With the sets theory from previous, we can define ordered pairs/Cartesian product:

Hence the definition of Cartesian product is

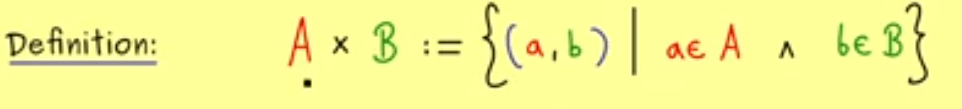
Then we can define subset using the sets theory and the Cartesian product just learned/defined

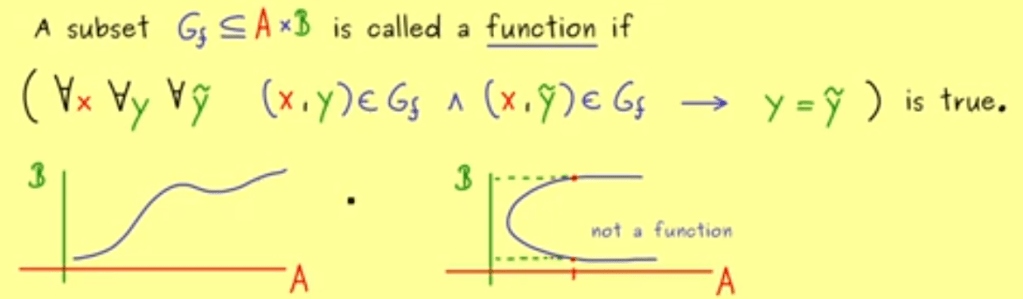
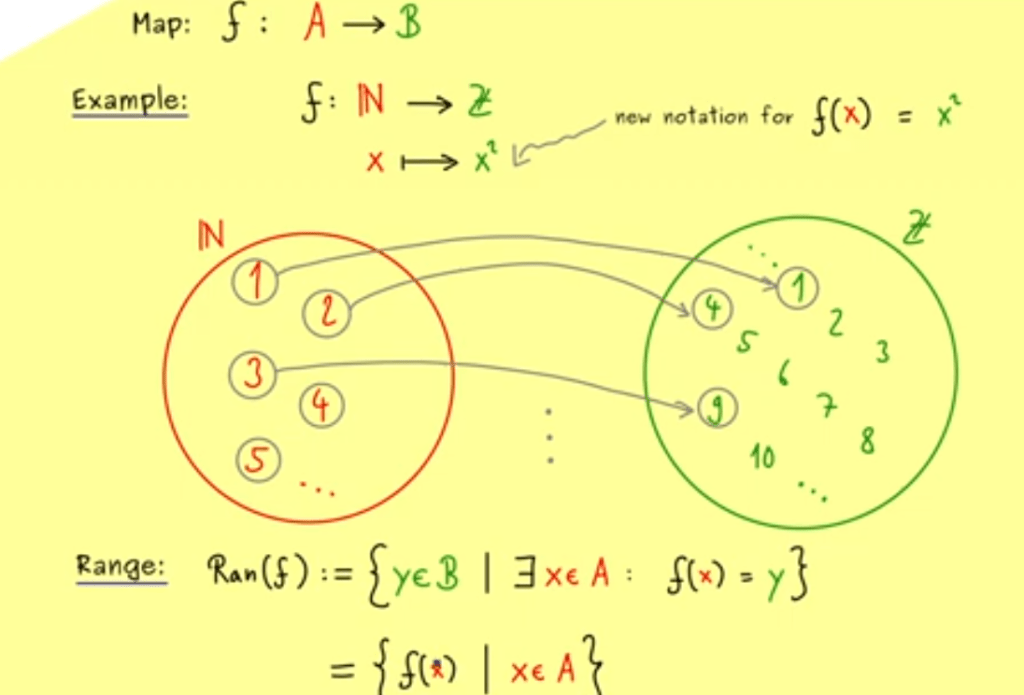
Based on function we define map

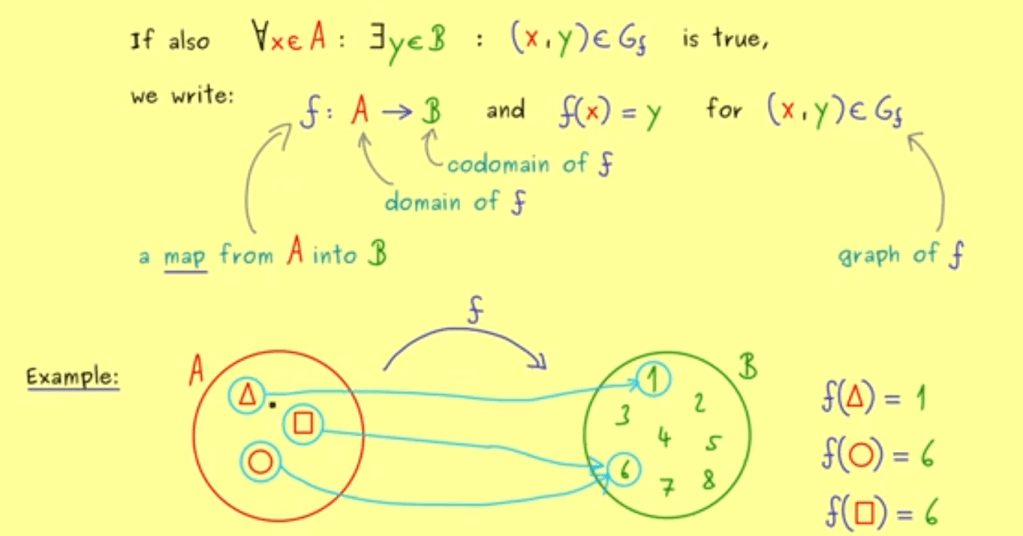
for example the map from Natural number set to Integral number set Z, we can define range(f) as below:

Apply the mindset of abstract set theory to rebuild the math edifice starting from understanding the “addition of natural numbers” logic. First how to define natural numbers from 1 to 2, to 3…, using set theory, we need to include 0 and define 0 as a set containing empty objects. Then set 1 is a set containing the empty set, i.e. 0. (this is nerve bending!)

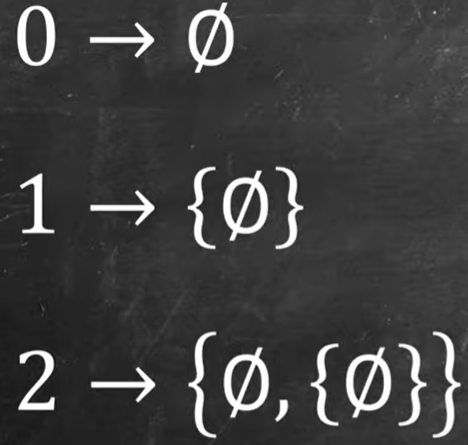
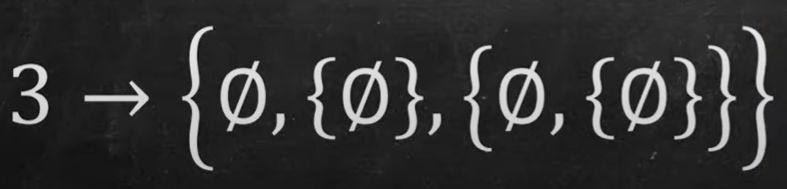
Why use set theory, it can also used to define functions:

Functions f: A -> B are sets with elements {x. {x, y}} where every element in A is associated with exactly one element in B.

Function of addition should be re-understood as

Generalizing to the Dedekind’s principle of recursive/inductive definition:

From Mathoma, expand knowledge on these concepts by thinking of all the subsets of powerset of powerset A as in below: it must be 2 raised to 2(two elements in powerset of A):

In his series of Number Theory the rest are:

ZFC Axioms
Russel’s Paradox
The Bogus Universal Set
Ordered Pairs and Cartisian Products
Relations
Functions and the Axiom of Choice
Equivalence Relations and classes
Natural Numbers and Induction
Peano Axioms/Systems and Transitive Sets
Isomorphism of Peano Systems
Natural Number Arithmetic
Ordering of the Natural Numbers
Constructing the Integers
Constructing the Rationsl Numbers
Real Numbers and Dedekind Cuts
Constructing the Complex Numbers
Quaternions and 3D Rotations
More on the Quaternions
Dedekind Cut Arithmetic
Decimal, Binary, and Dedekind Cuts
Dedekind Cuts for Complicated Numbers
Correspondence Between Number Systems
Equinumerosity and “Sizes” of Sets
The Rational Numbers are Countably Infinite
Infinite Binary Sequences and Cantor’s Diagonal Argument
The Complex Numbers are Uncountably Infinite