Approximation Theory, closely related to optimization is a core concept in mathematics. Let’s start from the very basic Metric space first.
A metric space is a set such that for every x and y in the set there is a function d(x,y) which describes the distance between them. Simply put it is a set together with a metric on the set. It satisfies 4 properties:
- the distance from A to B is zero if and only if A and B are the same point,
- the distance between two distinct points is positive,
- the distance from A to B is the same as the distance from B to A, and
- the distance from A to B is less than or equal to the distance from A to B via any third point C.
Normed Linear Space is a subset of metric space composed of a pair of objects (V, d) where V is a vector space and d is a function d:V x V –> R. d(x, y) is called the norm of V and is written as ||x-y||.

So there is the concepts of L1 norm and L2 norm. L2 norm is more familiar as below, while L1 is simple addition ||X||1 = |X1| + |X2|.
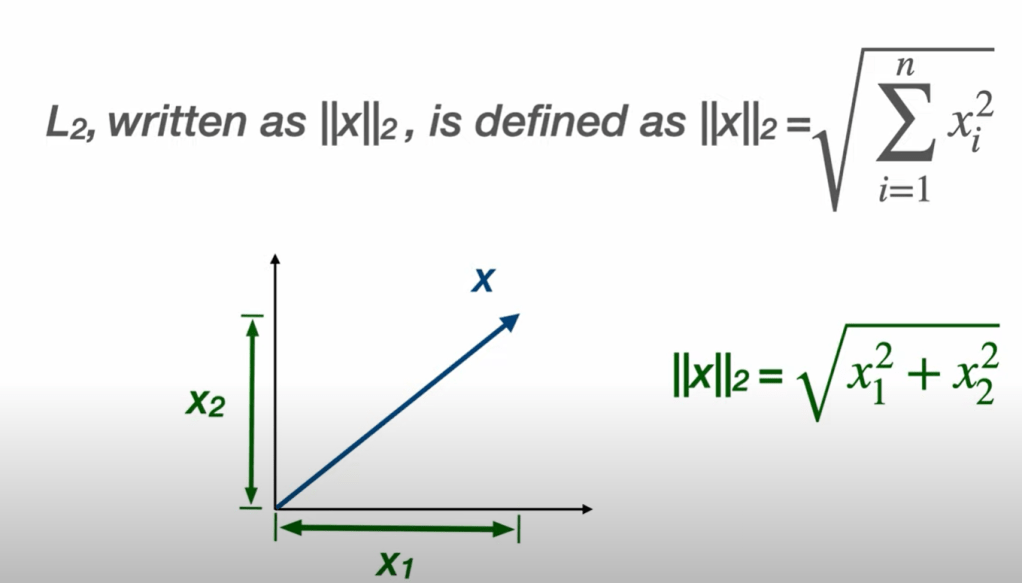
Generalizing we can define Lp norm. Drawing it geometrically using an example of ||X||p = 1, we get below incremental view of what it look likes from 1 to infinity.

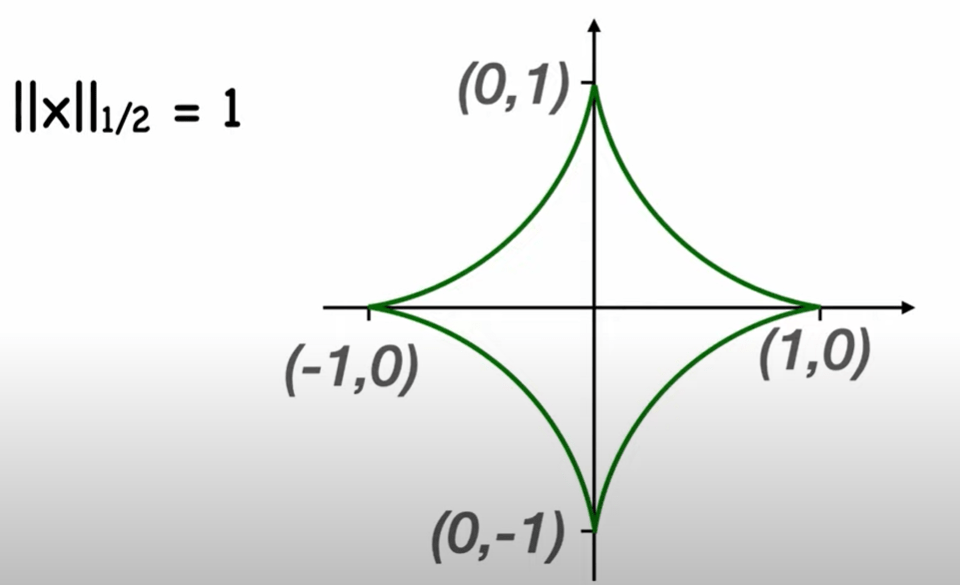
What about Norm half?
The Lp norm can be applied to continuous functions, which are vectors, or live in norm vector space.
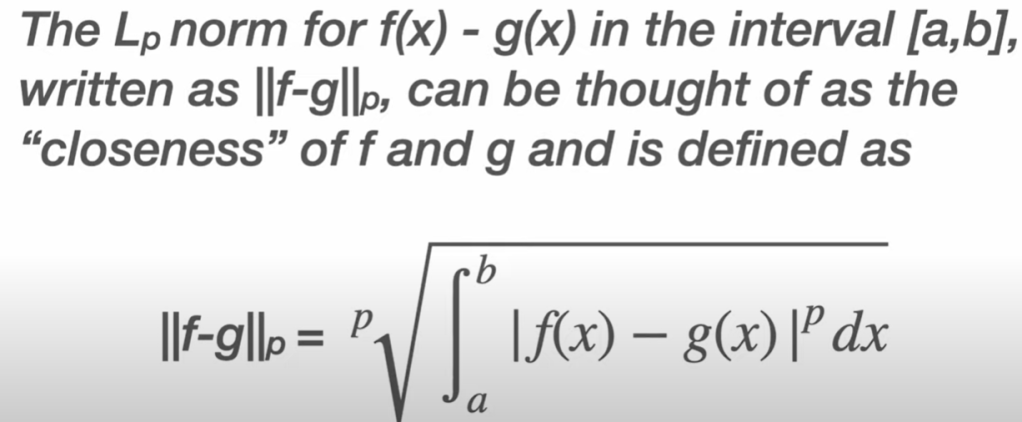
To get the hang of it, we can get a visual representation when p = 2:
