Having basic understanding of topology, especially on convergence and continuity, now we move onto the below topics, which we’ve applied in other subjects calculus and linear algebra without actually questioning how and why they are defined.

First, distance, the definition of distance is: let E be a set and d be a funtion d: ExE -> R, d is called a distance function on E if

If above four criteria are met, d is distance function, then (E, d) is a metric space.

Examples help understand, a typical Euclid distance we learned, or later expanded, the concept of norm, to extend more, the below two are also distance

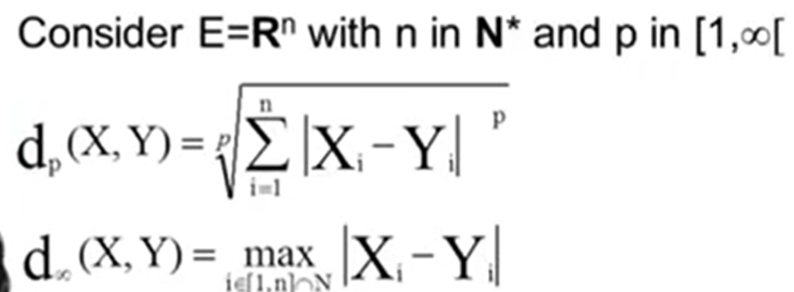
Let E be the set of metro stations in Paris and in Washington DC, and d(x,y) be the average time to get from x in E to y in E, using the fastest way. the d is a distance in former case but not in latter one because the loops in Paris metro map, so

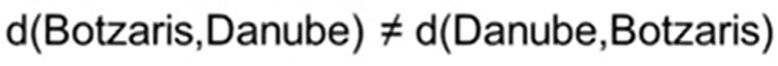
Another question: