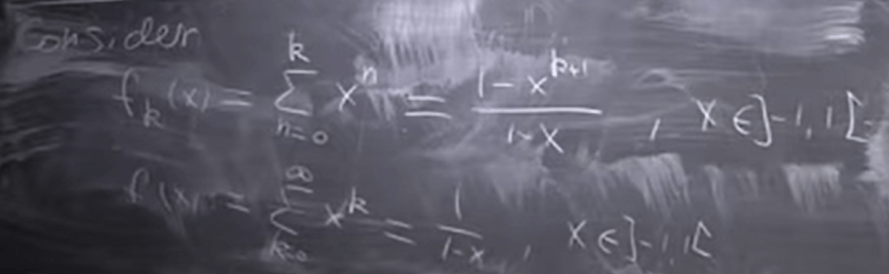Along the same pattern as the function of distance and then notion of metric space, so is the function of “norm” and then the notion of “normed vector space”.

This looks quite like distance but is not distance. I gather in linear algebra, the two are regarded inter-changeable, so it’s bit confusing to topology learning stage. Now given the precise definition of norm, we found the scope is much enlarged too, for example, test if N(u) below is a norm?
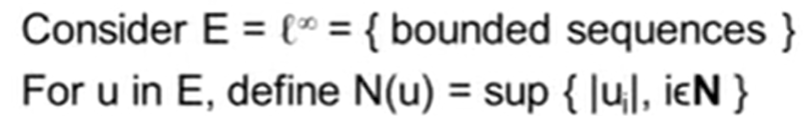
Normed vector space can lead to metric space. Simple, because if (E, N) is a normed space, given x, and y in E, we can define d(x, y) = N(y-x), then (E, d) is a metric space.
The scopes are
Now converging sequence in a normed vector space can be interpreted as

The norm is a continuous function.
Definition of strength of norm. A stronger norm will provide a stronger topology.
Definition of norm equivalence.
Switching to professor Ole Christensen German at channel DTUdk.
Concept of Supreme E belong to R, E is bounded above if there exists Superemum over E. denote the smallest such beta. short named SupE. It could be infinity, or not bounded above. for example
f(x) = -x^2 + 2x, x belong to [0, 3[, the supreme value is attained.
Another example of norm vector space is
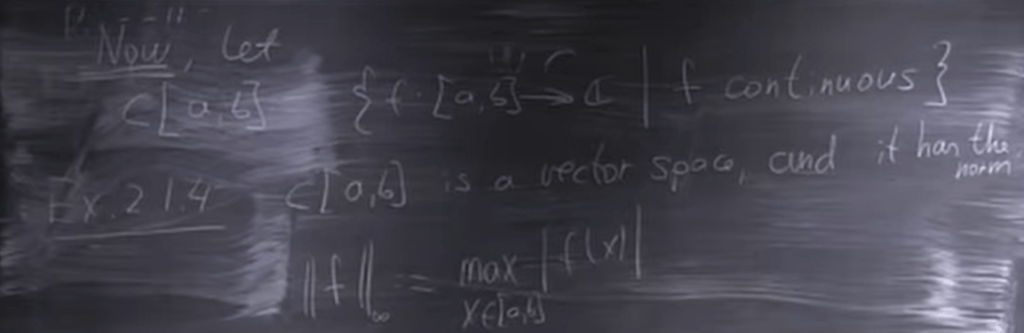
Details are given in proving, very informative for novice guy to learn. Rigorous logic is applied, for example the below part to prove the third point – triangle inequality.
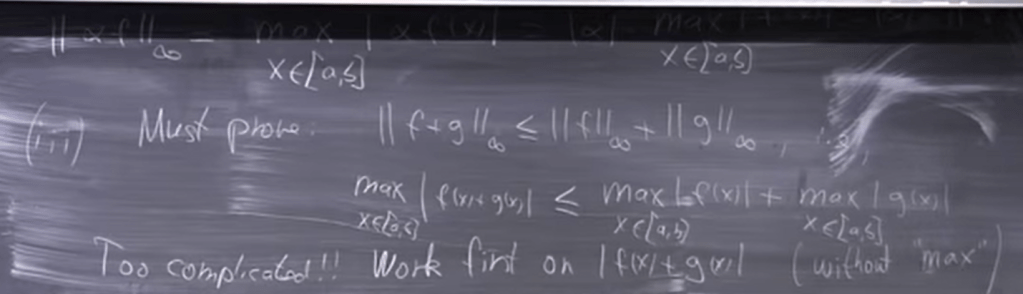
Another example in proving a function is in norm vector space: