Hilbert might be the one came up with General Relativity if purely stressing the math element in it.

The content to follow is

Given what we know about linear operator and inner product, let’s first learn and define Bilinear Form:

Since this Bilinear Form is a function or a map, no wonder the properties listed above remind me of Matrix, which is also a mapping or function except it’s effected on two elements in X space, turned into R. Inner product that we’ve been familiar with is a definite positive symmetric bilinear form on X, X being a vector space.

OK, the below form is usual or trivial inner product, we’ve seen a lot.

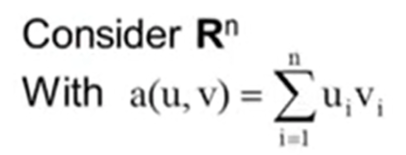
Not so familiar to identify, but also is a form of inner product for functions is below

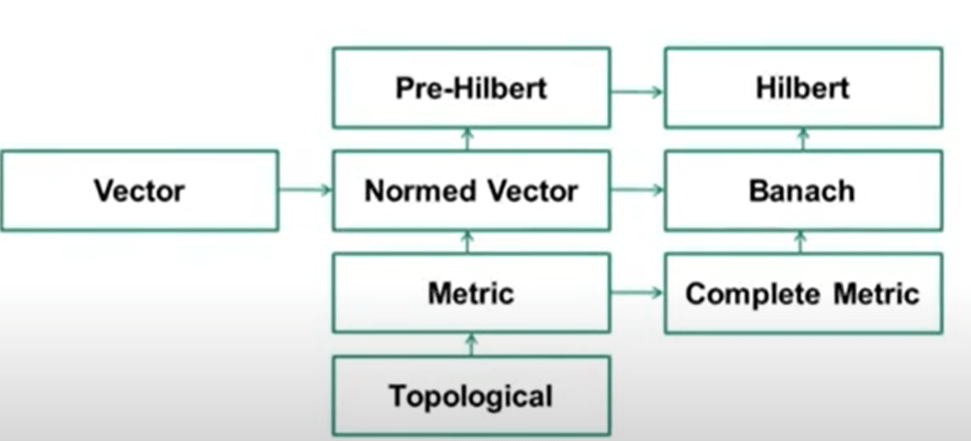
From pre-Hilbert Space to normed vector space.

Now turning to what is the definition of Hilbert Space? It is a complete pre-Hilbert Space. Or a Banach space with inner product.