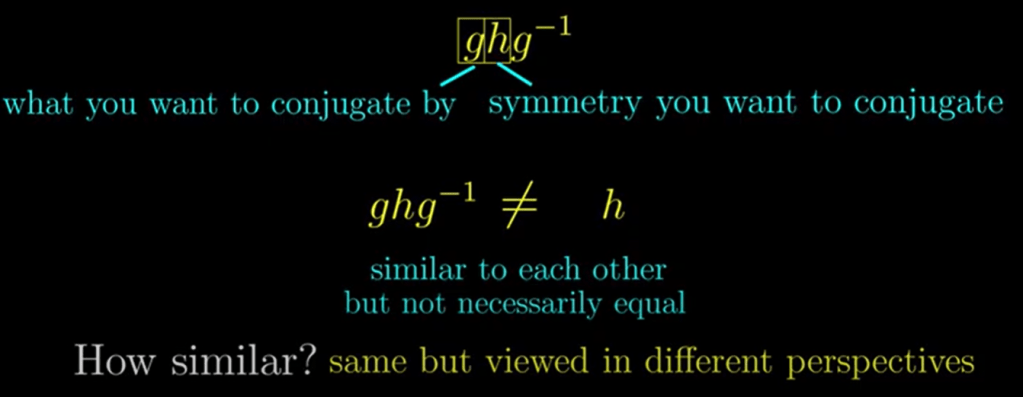Groups, per Galois, is conceived from symmetries (symmetry is precisely defined as keeping the distance and object), what symmetries do to the object is the group action, for example, below sigma action makes the object rotate around axis through 1 has the following results

Group theory is to study “group structure”, or how symmetries relate to each other. For example real number set/group has infinite symmetries, while the tetrahedron only has finite symmetries.

To generalize, orbit-stabiliser theorem is presented.

Lagrange’s theorem is tbd

Then to grasp concept of conjugation