00:00 – Banach Spaces; 06:30 – Cauchy Sequences; 12:00 – Def: Banach Space; 15:45 – Examples; 17:15 – C[A,B] Is Banach With Proof; 36:30 – Ex: Sequence Space L^1(N); 46:45 – Sequence Space L^p(N);

We’ve learned the concept of converging as

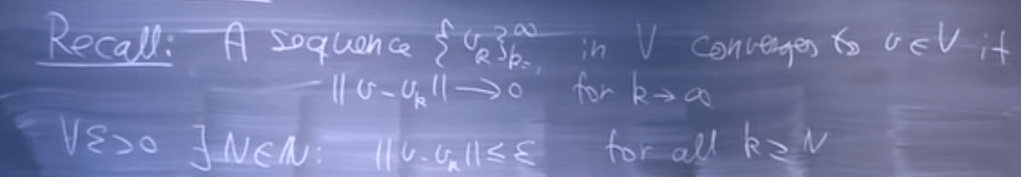
It would be hard to utilize with above concept, so tweak a bit by introducing a specific v_l. Then we define every convergent sequence is Cauchy Sequence.

A Banach Space is a normed vector space V in which all Cauchy Sequences converges to some v in V. We need to prove it. so write down

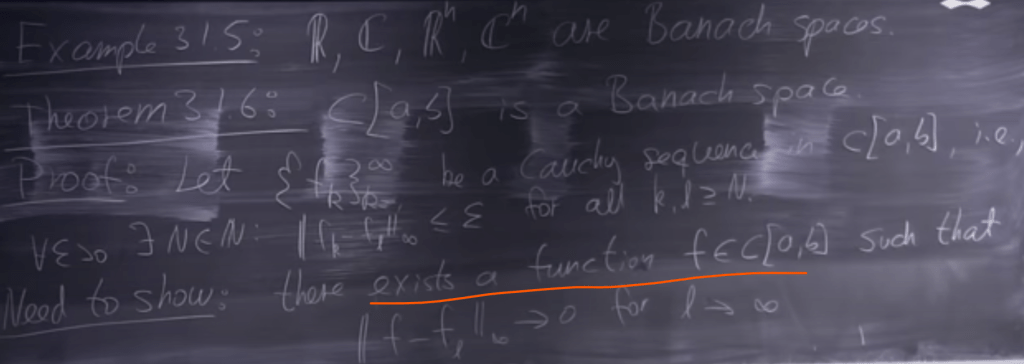
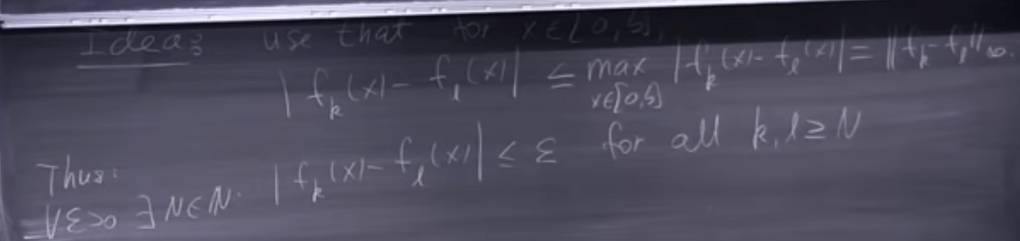
Be very careful the notations here. There are two concepts here, the interval between a and b, and the sequence denoted by k, k from 0 to infinity in N.

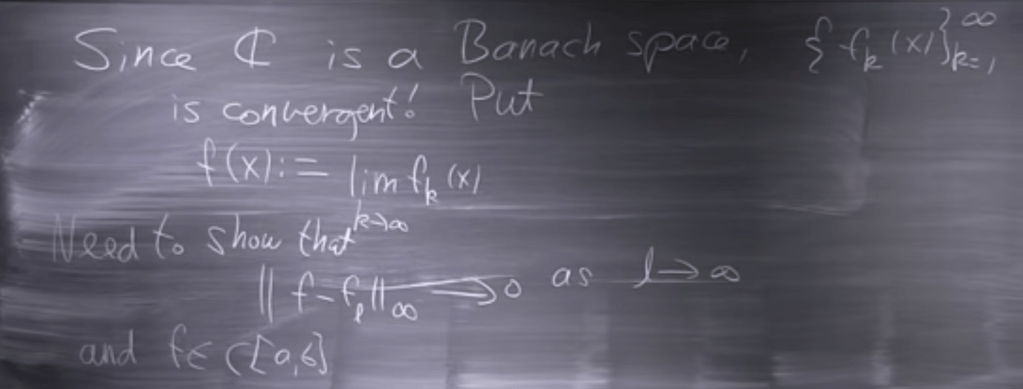
Whether this f(x) is Cauchy Sequence or in Banach Space needs to be proved by satisfying above two criteria.

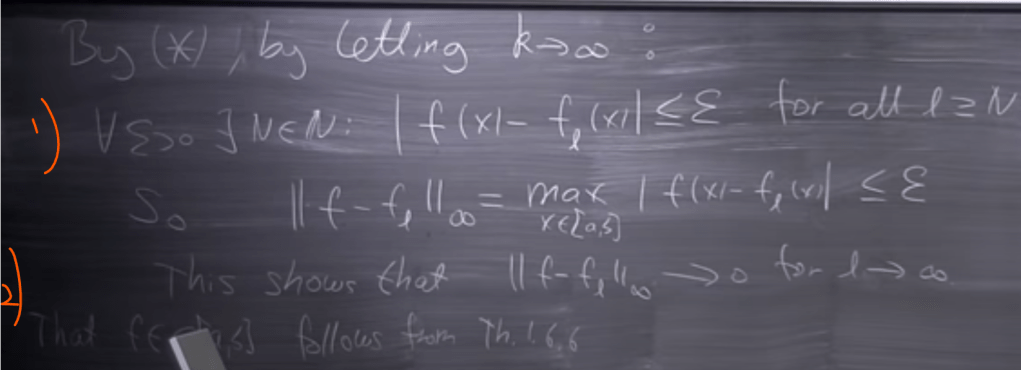
There is another Banach Space example

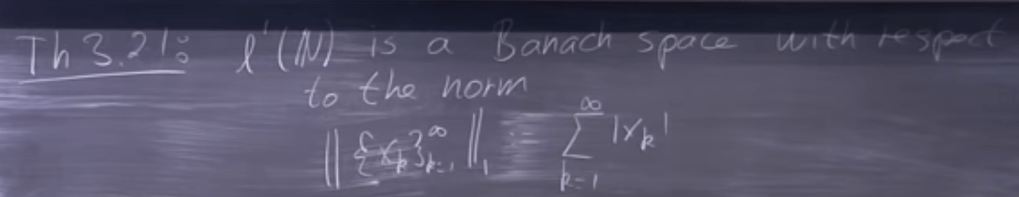
Generalizing to the following: