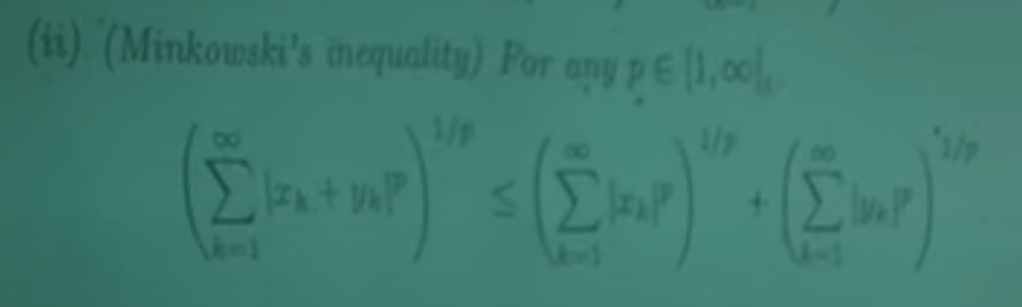00:00 – More On L^p(N); 06:30 – Minkowski Inequality; 08:30 – Linear Operators; 13:00 – Bounded Linear Operators; 15:00 – Operator Norm; 19:45 – T:C[0,2]-→C[0,2],Tf(X)=X^2*F(X); 35:00 – Operator On L^p;

Continue on the generalized idea of norm l²(N) which is a Banach space with respect to the norm.

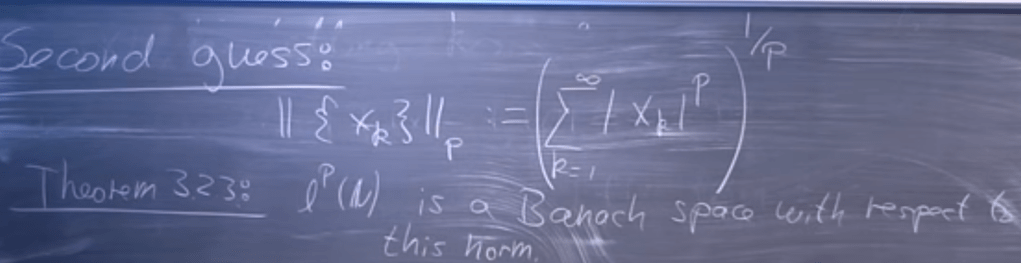
Linear Matrix T that transform a vector in Space V to another vector also in Space V is bounded if below is satisfied and the smallest value of k is called operator norm on T. Note the two Space can be of different dimensions.

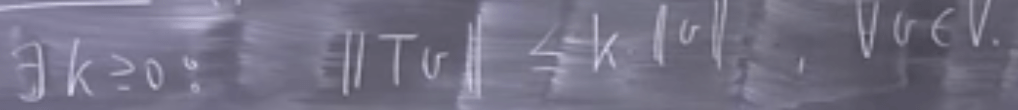
Moving on to consider a linear matrix/transformation T that maps continuous function on interval 0 and 2 to a continuous function on interval 0 and 2:

The first one and second point are easy to prove, as to the third one, it’s still unfamiliar, so need to go over how to prove “bounded”, Norm is the critical concept here.

Another example is

Again, after reviewing it is well defined we then need to prove it’s linear and bounded.

Minkowski’s inequality will be used to prove “T is well defined”.