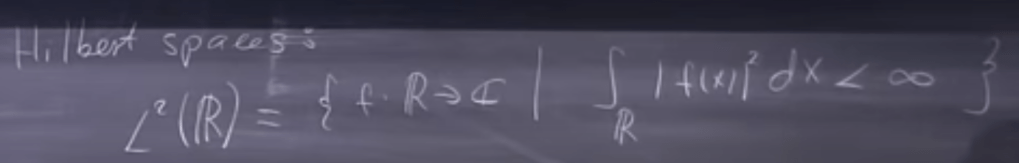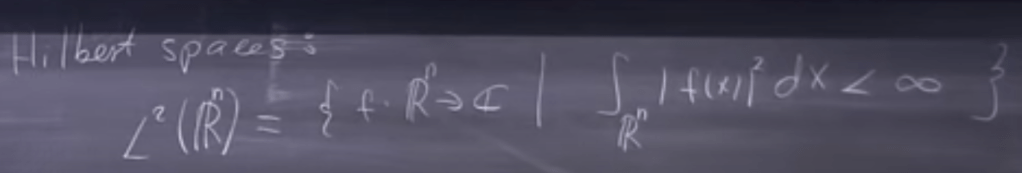03:45 – R^n Is Banach; 07:00 – Inner Product; 14:00 – Example: C^n; 22:45 – What About ←V,Aw+Bu→; 25:30 – R^2; 28:15 – Cauchy Schwarz Inequality; 30:15 – Inner Product Induces A Norm; 41:30 – Inner Product On Real Spaces; 43:45 – Important Properties Of An Inner Product; 00:00 – Def: Hilbert Space; 05:00 – New Example Of A Hilbert Space; 15:15 – Operators On Hilbert Spaces; 20:00 – Example 1; 24:00 – Example 2; 38:30 – Riesz Representation Theorem; 43:00 – Concerning Physics;

Recap on Banach space: note the definition contains both sequence converge to infinity (summation of elements) and with respect to (w.r.t) norm of elements is equal to the summation of elements raised by 1/p. so the three criteria of norm is fulfilled.

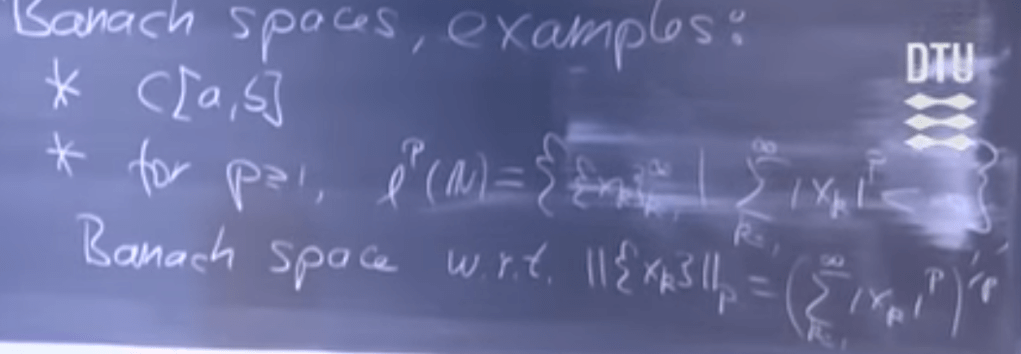
Then we go over the inner product(scaler product) concept in linear algebra, generalizing it to complex number space

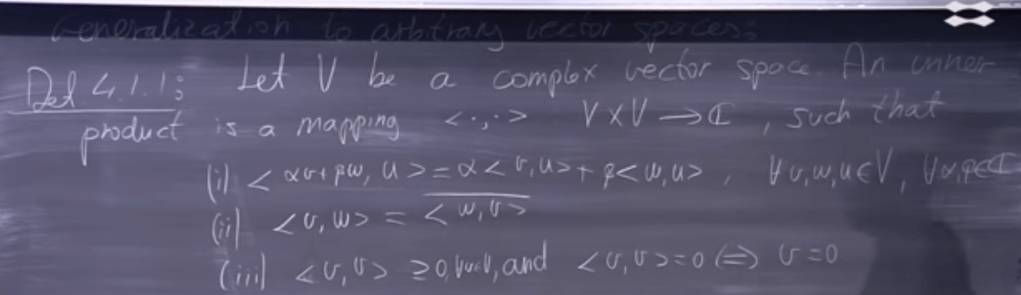
So to have C^n, like R^n, is a vector space with above inner product properties, we write out as below and then try to prove one by one.

Further, we recall in R^n space,

A very important property of inner product is the relationship between norms and inner product, if you know inner product you can recover norms, vice versa. And then the Parallelogram law for all v, w in space V,

If the parallelogram law is not satisfied, then the norm does not come from inner product.

Finally, bringing up the official definition of HILBERT SPACE:

R^n and C^n are Hilbert Space, what about infinitive number of R or C? According to previous concept of l²(N), it is a Hilbert Space w.r.t. the inner product form as below:

But is it? Mathematician always will prove it in rigorous manner. (follow the same proving R^n is Hilbert Space above)

Now to learn “linear operator”, first simple one mapping from Hilbert space to complex number space:

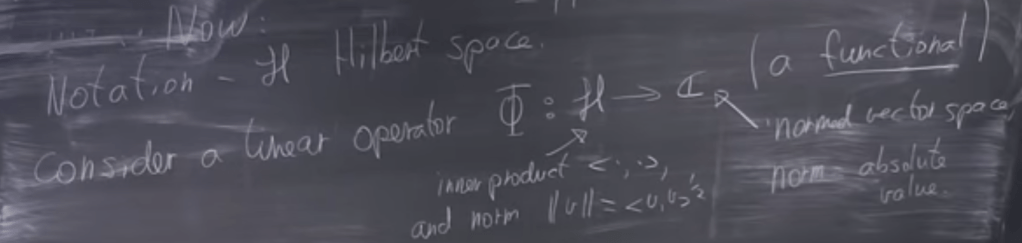
We would like to know if it is a “bounded” linear operator, so what’s the definition of bounded linear operator?

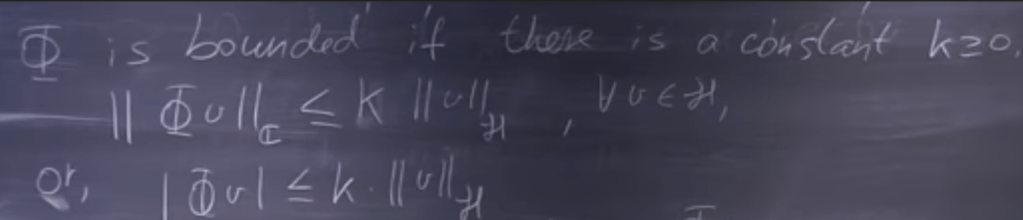
The proving in details should go over again in depth later on.

Next, theorem 443 states that “all bounded functionals have the form in direct inner product of another vector say w:

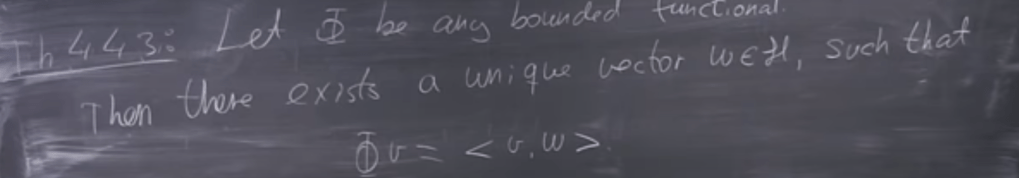
To connect the abstract math here to real world application – physics, the below Hilbert Space is defined as notated in capital L rather than small case l: