04:30 – Normed Vector Spaces; 08:30 – The Adjoint Operator; 18:30 – Theorem 4.5.1; 19:30 – Proof; 24:00 – Lema 4.4.2; 32:30 – Example Week 2; 12:45 – Definition Inverse Of T; 13:45 – Exercise 4.19; 20:15 – Basis; 20:45 – Recall; Topological, Metric Space, Normed Vector Space, Banach Space and Hilbert Space.

In mathematics, specifically in operator theory, each linear operator  on a Euclidean vector space defines a Hermitian adjoint (or adjoint) operator  on that space according to the rule

here Adjoint operator is linear operator following what have learned in previous blog

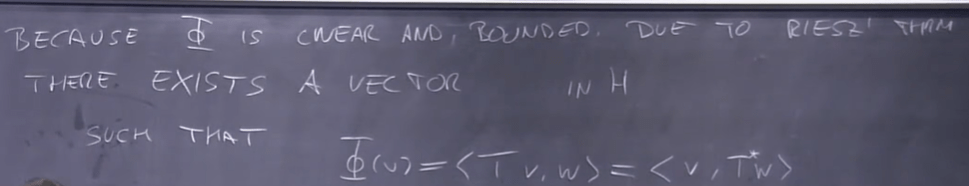
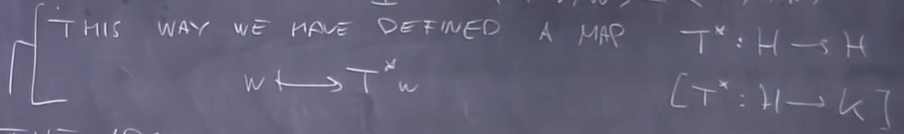
This T* mapping is the adjoint operator and is linear and bounded, and it needs to be proved.

Now apply it to an actual example

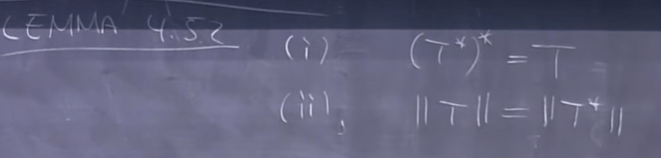
for the special case where the hilbert space is in R^n, unitary is orthogonal, self-adjoint is symmetric.