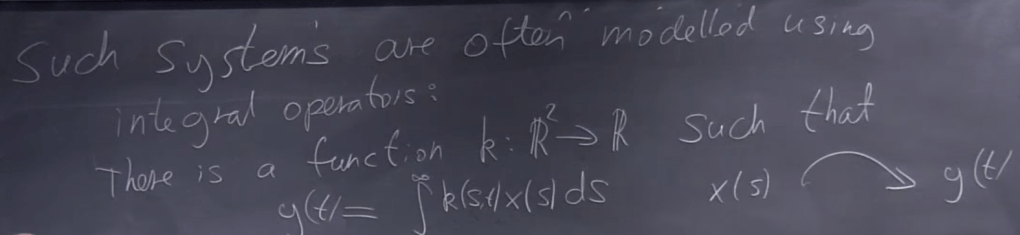In defining Lp space as below,

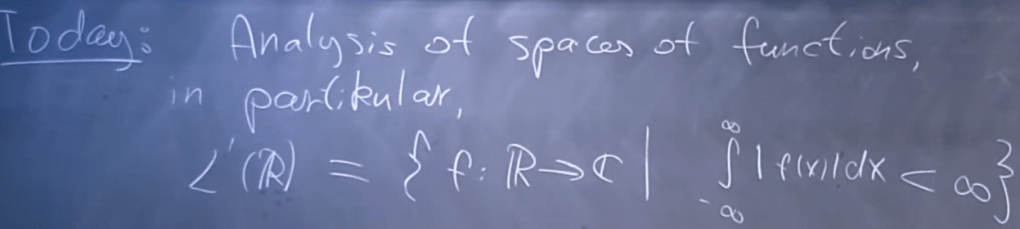
we say we can make sense of the integral such as the two examples, where the value to integrate is the absolute value. If you remove the absolute sign, the integration does not make any sense.

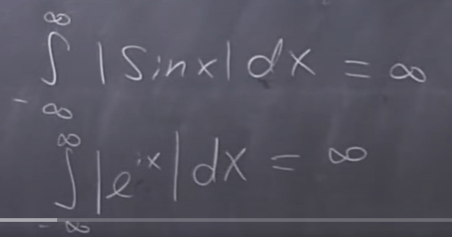
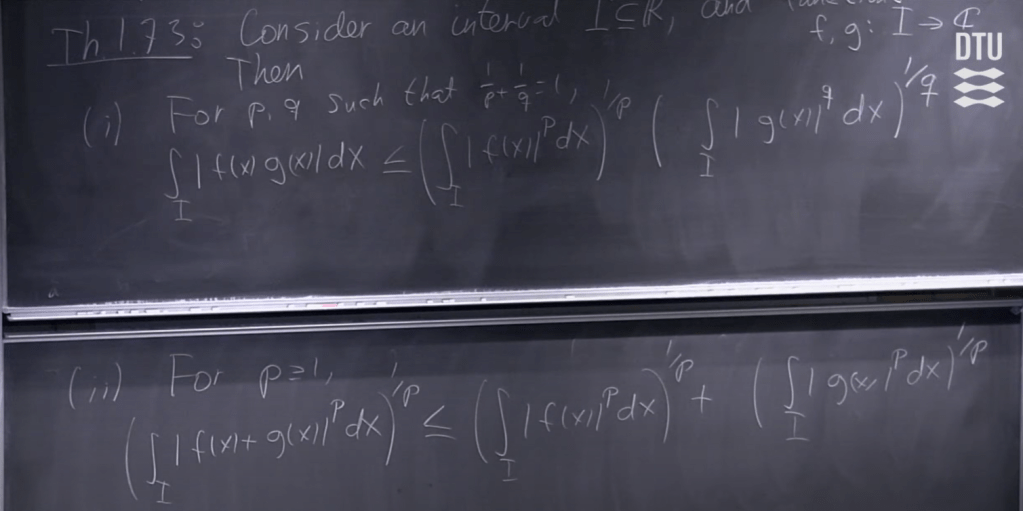
Ole emphasized over and over again about the premise or number 0 to check if the expression is well defined, see Lemma 172 below:

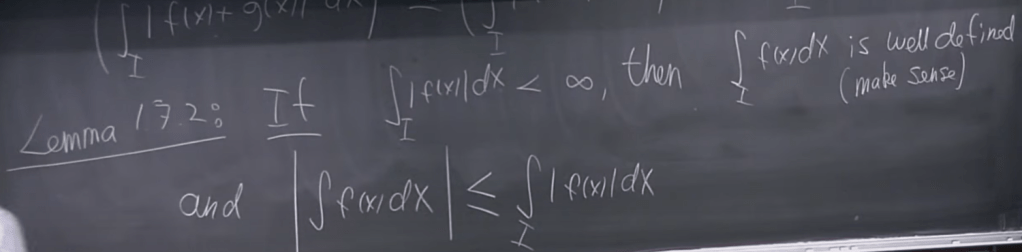
This is similar as absolute of a sequence is convergent infer that the sequence is convergent.

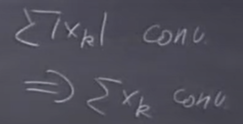
There is a very important concept of function called support of a function, consider an function mapping element in R to C, the support of f is the closure of the set of elements in R that fulfills mapping of them are not equal to zero. If the set is bounded, then we call it a “compact support of f”.

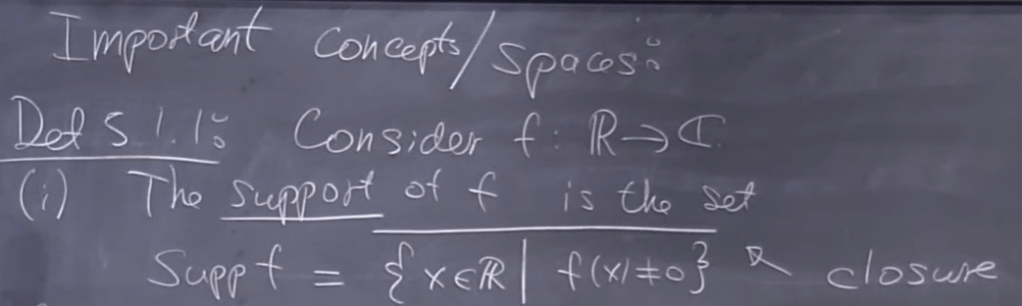
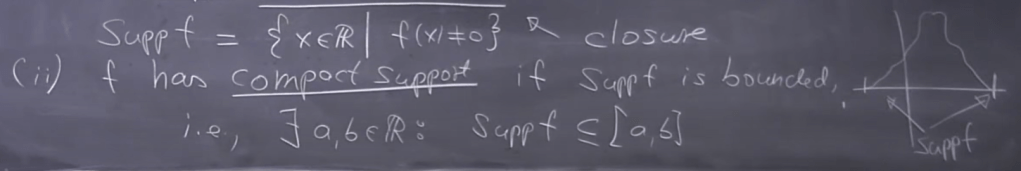
Showing vivid examples so you know why mathematicians/physicists came up with these definitions

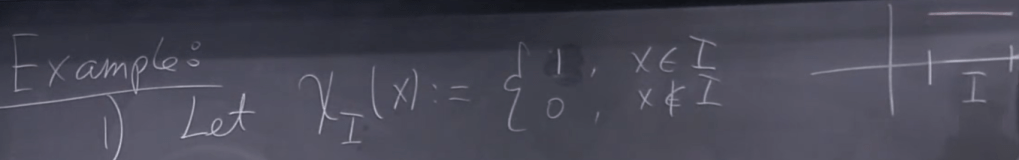
Another example

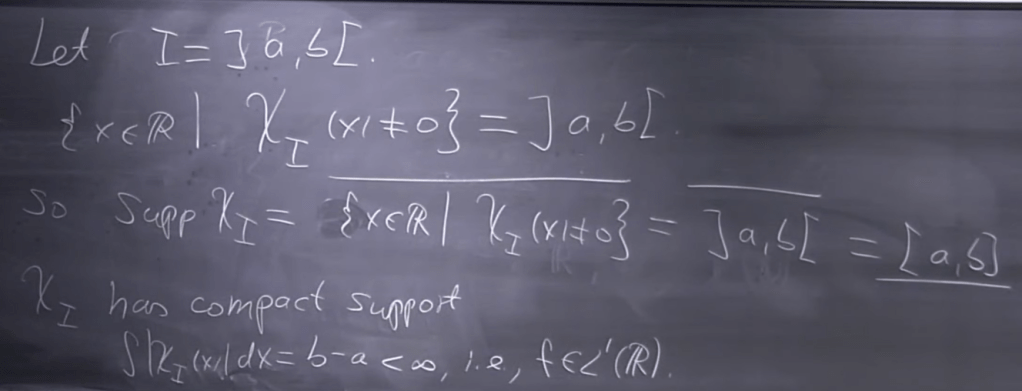
And because f is not continuous hence

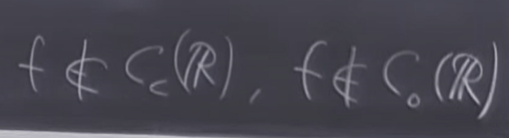
These concepts are abstract, especially compact/finite support: Finite support just means that the function’s domain has a finite number of values that produce non-zero values in the range. So f being integrable (i.e. finite valued) suggests that you can bound the domain of your simple function to finite support and still get your convergence.

This has finite/compact support:

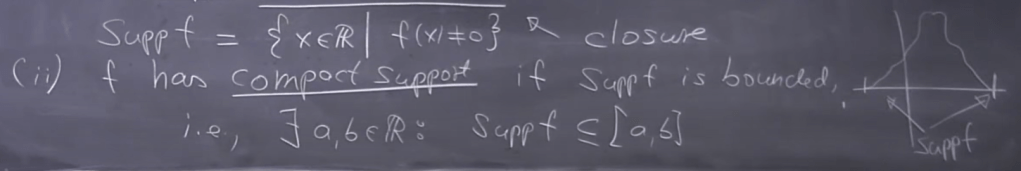
While this fifth function does not

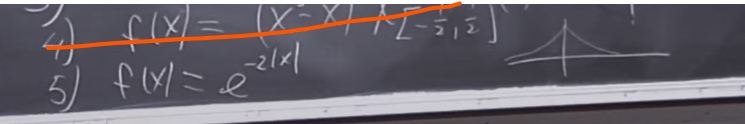
Cc(R) is subspace, also norm vector space but not Banach Space.

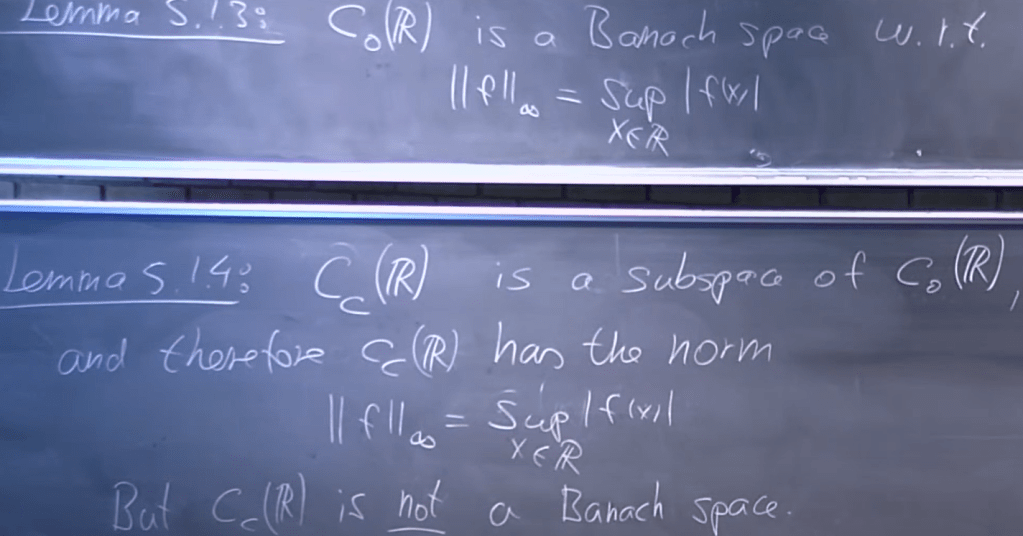
how to prove it? just need to find on converse example:

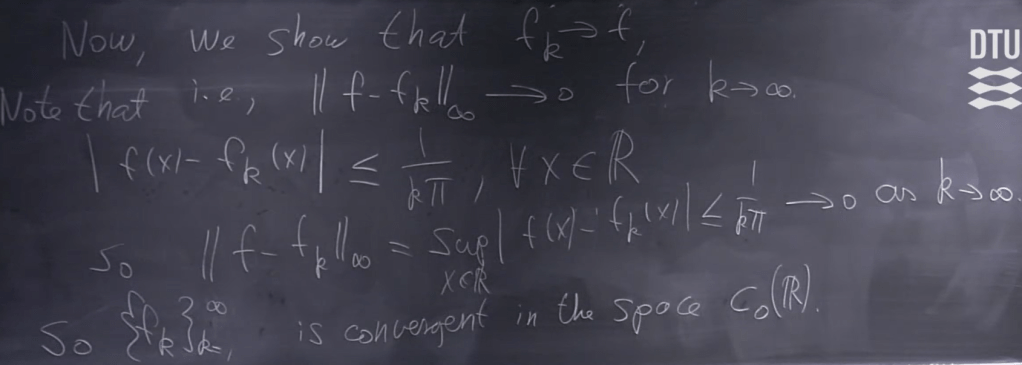
Why do we need to invent and grasp this??? Very useful in solving physics problem where “system” is defined to simplify and solve problems using “integral operators“.