When you zoom in, any complex equation can be transformed to linear problems.

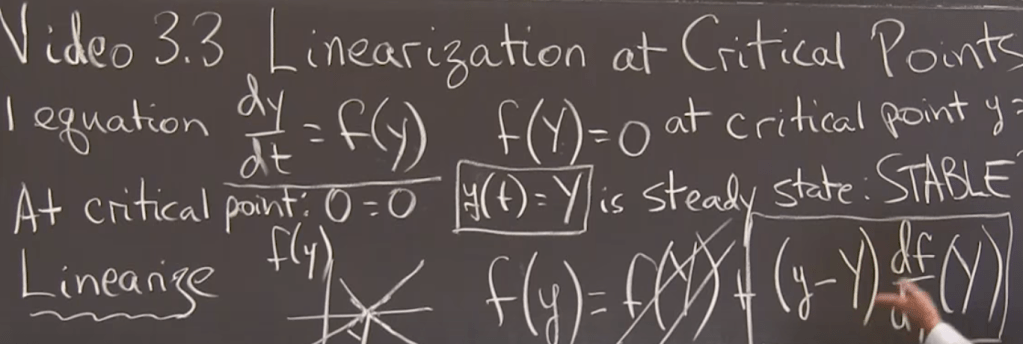
When we set f(Y)=0, we call this point is a critical point, then by studying the dirivative at this point, if it’s >0, it’s unstable, otherwise it’s stable because the exponential decay to infinite small.

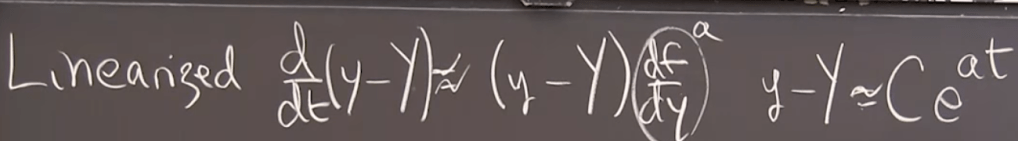
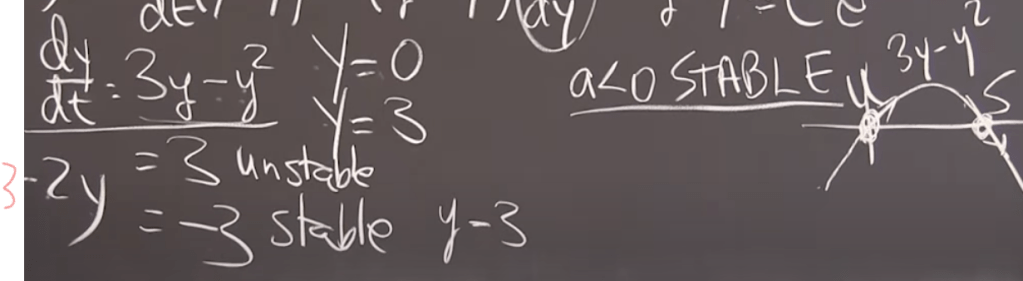
Another example where we have two equations:

A typical and interesting example is the population dynamics of rabbits and foxes, predators and preys. There are two critical points, Y=0, Z=0 and Y=1, Z=1.

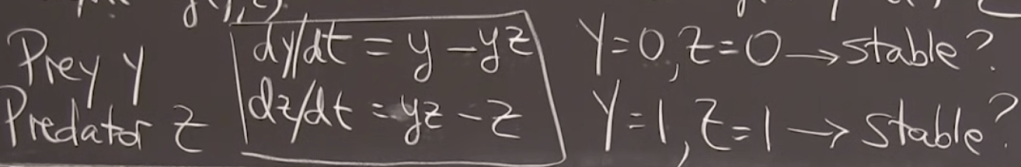
When Y=Z=0 turns out it’s a saddle point. While at Y=Z=1, let’s zoom in to investigate and find it’s a Center Neutral.

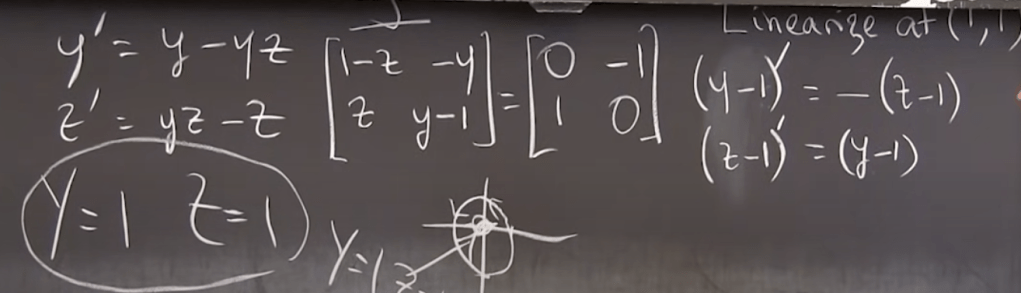
Now it’s crystal clear that the second order DE is equivalent to 2×2 matrix problem so evaluating the eigen value leads to solving the DE:

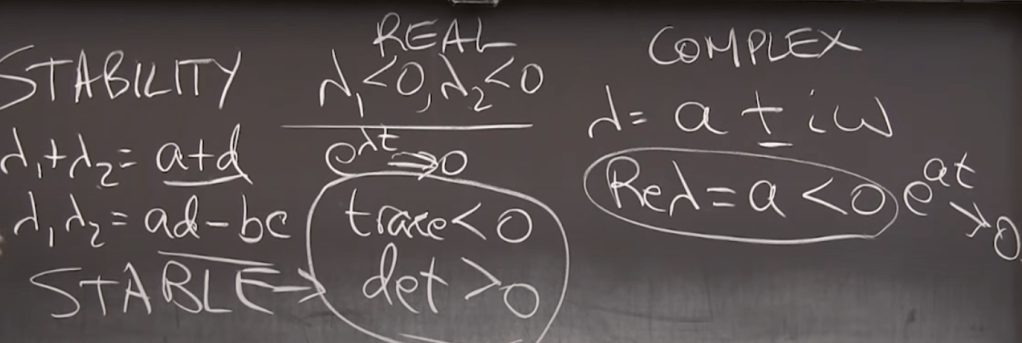
What’s essential is to evaluate if the solution is winding down to infinite small – we call it STABLE.

What about a more complex case like in three variable form, we’ll use the eigen values to evaluate stability of the system too.

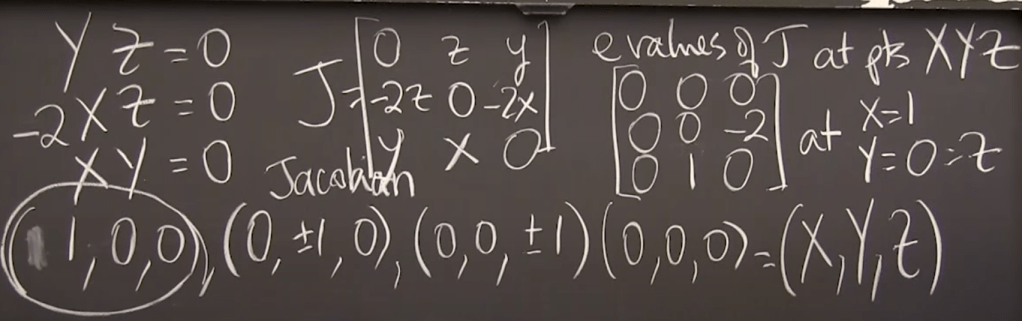
So when the middle one is 1, we calculate the eigen value could be 1 and -1 and the positive 1 leads to unstable situation.