The Lorentz transformations are specific to inertial frames of reference (non-accelerating frames), while the Poincaré transformations are more general and include both inertial and non-inertial frames of reference.

The key observation/postulates by Einstein is c = dx/dt = dx’/dt’, everything goes from there.

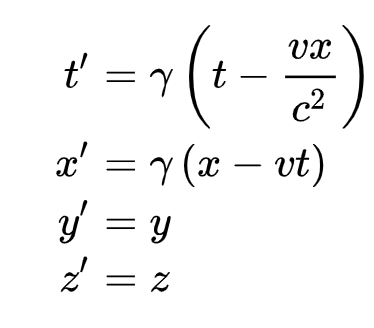
In special relativity, a boost is a transformation that changes the velocity of a system. The boost operator is a mathematical representation of this transformation. The boost operator is a mathematical representation of a physical transformation and only has a meaning in the context of special relativity.

n mathematics, a Lie group is a type of smooth and continuous group that is also a smooth manifold. Lie groups are named after the mathematician Sophus Lie, who first studied them in the 19th century.

A group is a set of elements with a binary operation that satisfies certain properties such as associativity and the existence of an identity element. In a Lie group, the group operation is a smooth and continuous function, and the group itself is a smooth manifold. This means that the group elements can be continuously and smoothly varied, and the group operation can be continuously and smoothly varied as well.

A Lie group has a Lie algebra, which is the tangent space of the Lie group at the identity element. Lie algebra can be visualized as the space of infinitesimal transformations of the group. The Lie algebra is generated by a set of basis elements, called Lie algebra generators, which satisfy a set of commutation relations called Lie algebra.

Examples of Lie groups include the special orthogonal group SO(3) which describes the rotations of a 3D object, the special linear group SL(2,C) which describe the Lorentz transformations in special relativity, and the unitary group U(n) which describes the unitary transformations in quantum mechanics.

In physics, spinors are mathematical objects that are used to represent the wave function of particles with spin. The spin of a particle refers to its intrinsic angular momentum, and spinors are used to represent the possible states of a particle with spin.

Weyl spinors and Dirac spinors are two different types of spinors that are used to represent the wave function of particles in physics.

Weyl spinors are two-component spinors that are used to represent massless particles such as photons and neutrinos. They are named after the physicist Hermann Weyl, who first introduced them in the 1920s. Weyl spinors are characterized by a left-handed and a right-handed component, and they transform differently under Lorentz transformations.

Dirac spinors, on the other hand, are four-component spinors that are used to represent massive particles such as electrons and quarks. They were introduced by Paul Dirac in the 1930s, and they are used to represent the wave function of particles with spin-1/2. Dirac spinors are characterized by a positive-energy and a negative-energy component, and they transform in a certain way under Lorentz transformations.

The Schrödinger equation and the Dirac equation are both used to describe the behavior of quantum mechanical systems, but the Schrödinger equation is used for non-relativistic systems, and the Dirac equation is used for relativistic systems, particularly for spin-1/2 particles such as electrons and quarks. The Schrödinger equation is a second-order partial differential equation, while the Dirac equation is a first-order partial differential equation. The Schrödinger equation doesn’t take into account the effects of special relativity, while the Dirac equation is fully relativistic.