When we say Density Operator, it’s usually in comparison to solve QM problems using Density Operator versus using familiar state vector approach. Why? because in a solving with mixed number of quantum states at the magnitude order of ^23, using density operator can make the complexity at linear level while using state vector would be quadratic.

Density operators, also known as density matrices, are commonly used in quantum mechanics to describe the state of a quantum system. They are used when the state of a system cannot be described by a pure state vector, but rather by a mixed state that is a probabilistic combination of pure states. This is particularly relevant in the study of quantum systems that are open and interacting with the environment, such as in quantum optics, quantum information theory, and quantum thermodynamics. The density operator is used to calculate probabilities for measurements and to evolve the state of the system over time.

The outer product is a special case of the more general tensor product operation, restricted to vectors to create a matrix. The tensor product works on spaces of any dimension to create higher order tensors.

Density operator is a generalization of the outer product that accounts for the statistical nature of quantum mechanics.

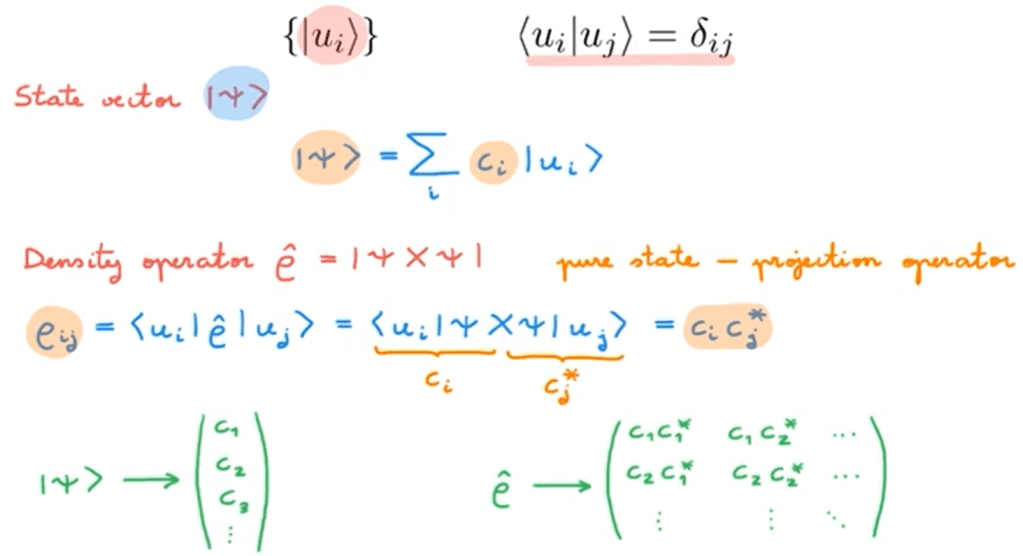
density operator is defined as the outer/projection/cross product of sai and sai. it can be thought of as another form of expressing in the right bottom equivalent to the form of left bottom “state vector”, so the following computation would be easier.

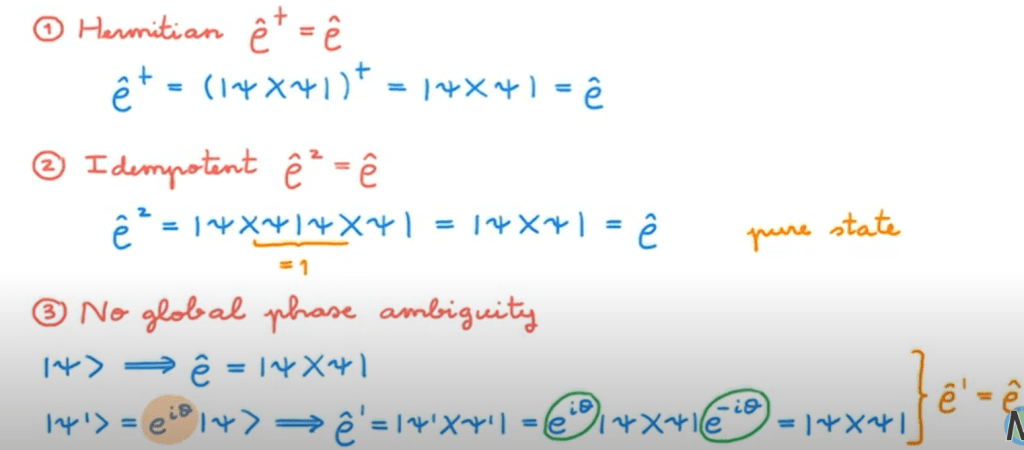
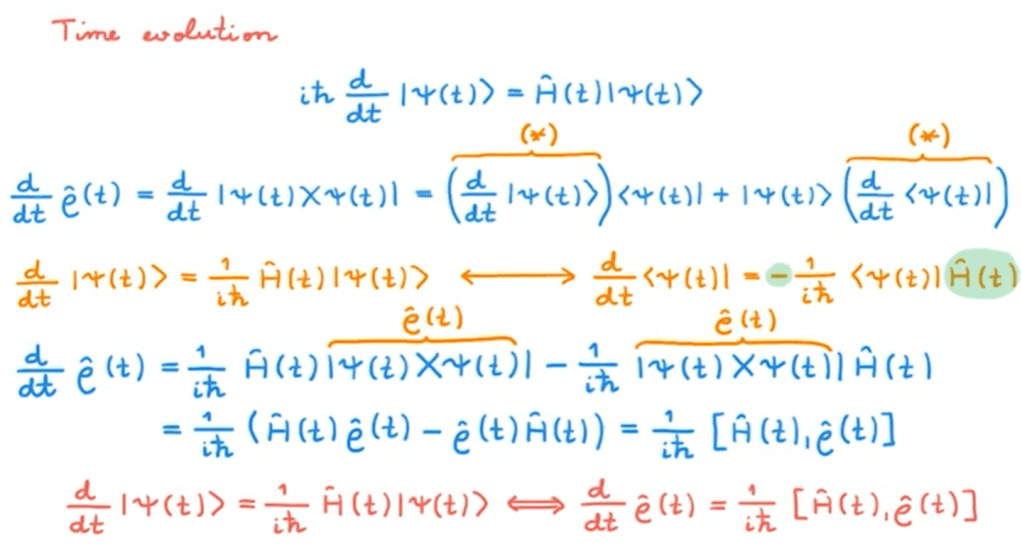
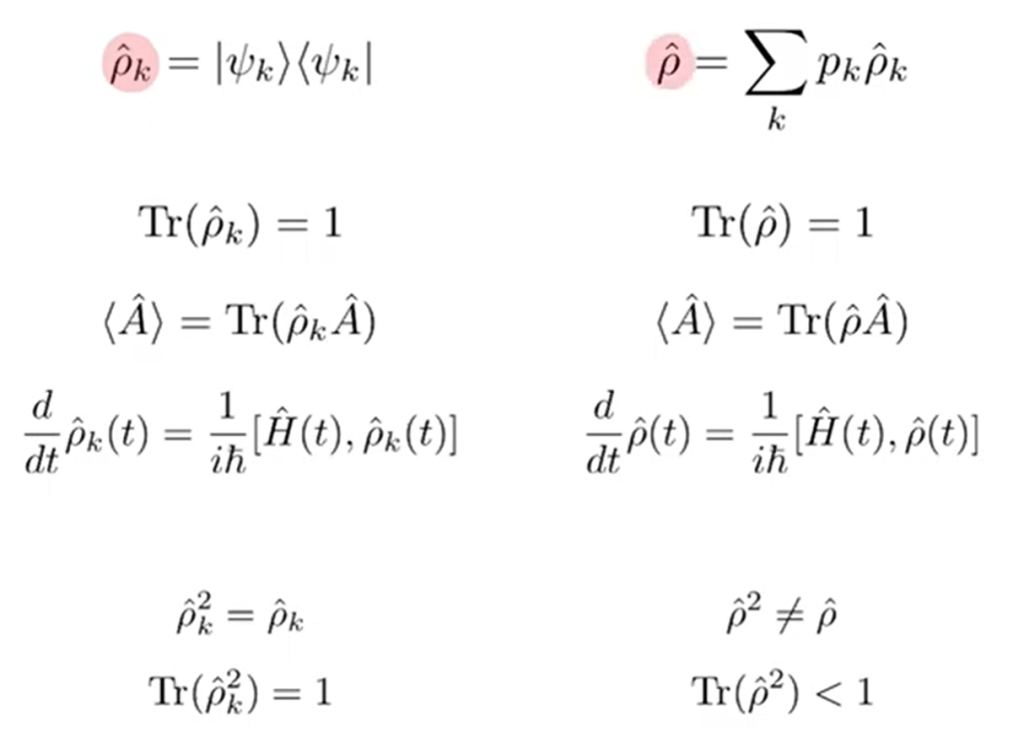
why the density operator is called the density operator in quantum mechanics?

In thermodynamics, the density refers to the number of particles per unit volume. Similarly in quantum statistical mechanics, the density operator contains information about the number of particles in each quantum state. So it represents a “density” in an abstract vector space.