EigenChris gives definition of Tensor on four levels. The last level is abstract as combination of covector and vectors. His explanation of covector and vector both as invariance is very informing. But another deep understanding of tensor as related to scalar and vector is truly illuminating.

It is explained by Gabriele in this playlist.

Vector is defined by a point P and direction, while Tensor T is defined by a point with two or more directions. That’s tensor! Pretty much derivative from vector. Vector and covector well also is similar or identical to some degree, just living in different spaces.

what is curl, starting from 2d curl by Khan academy:

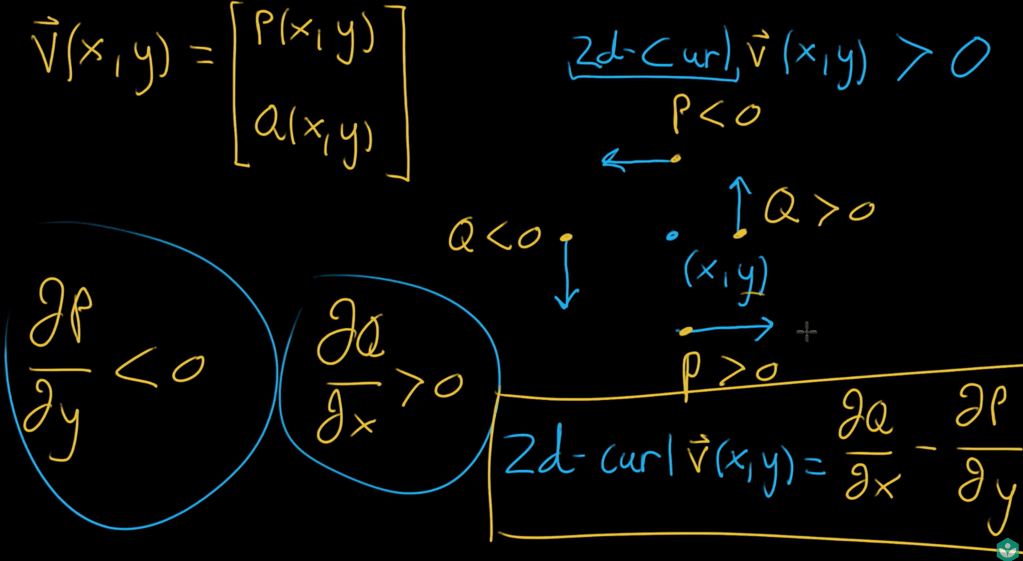
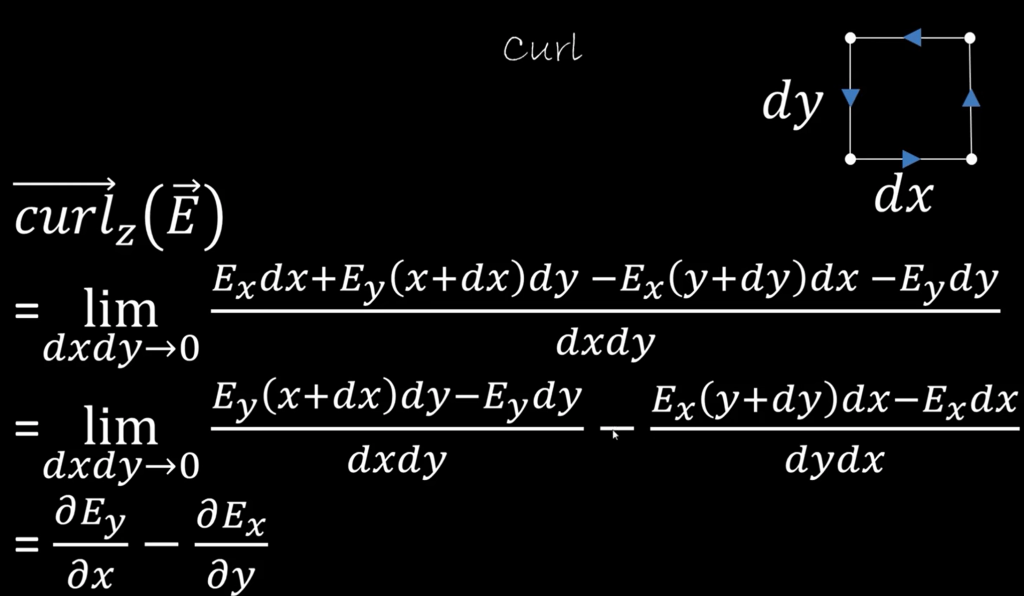
Curl is a tensor of rank n-2:

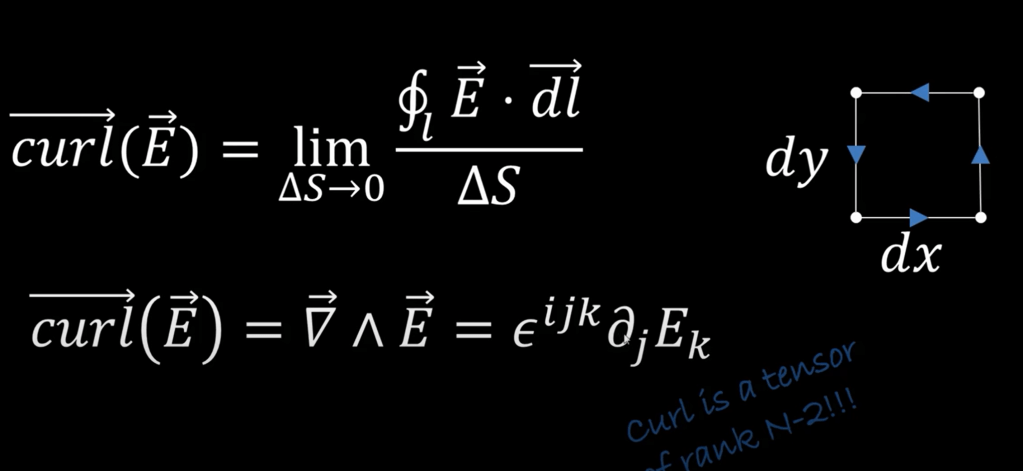
Adding on stress tensor: it’s useful in calculating stress on each face.

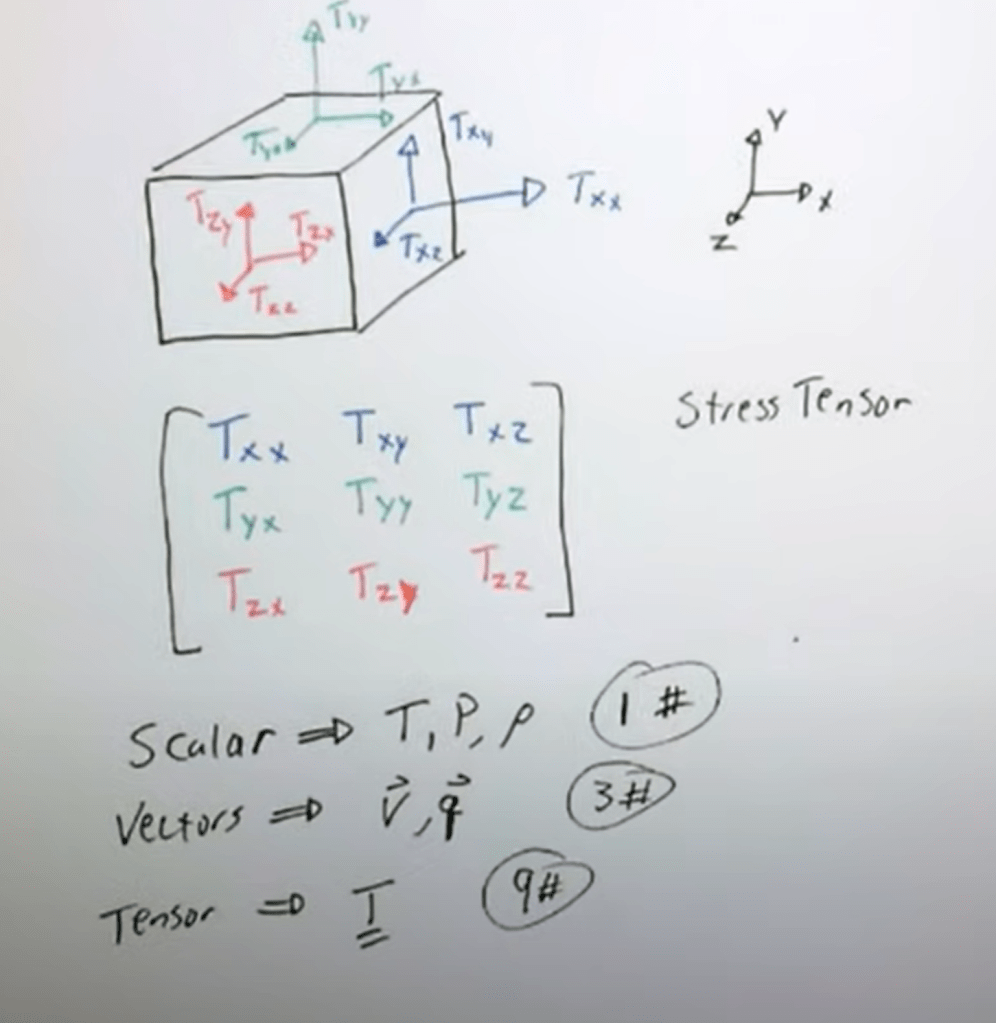
Scalar has 0 component/basis vectors to define, vector has 1 or multiple components, each needs 1 vector basis to define, hence vector is rank 1 tensor, tensor has 2 or multiple components, each needs 2 or more basis vectors, thus it’s rank2, rank3 et al.

Understanding went deeper:

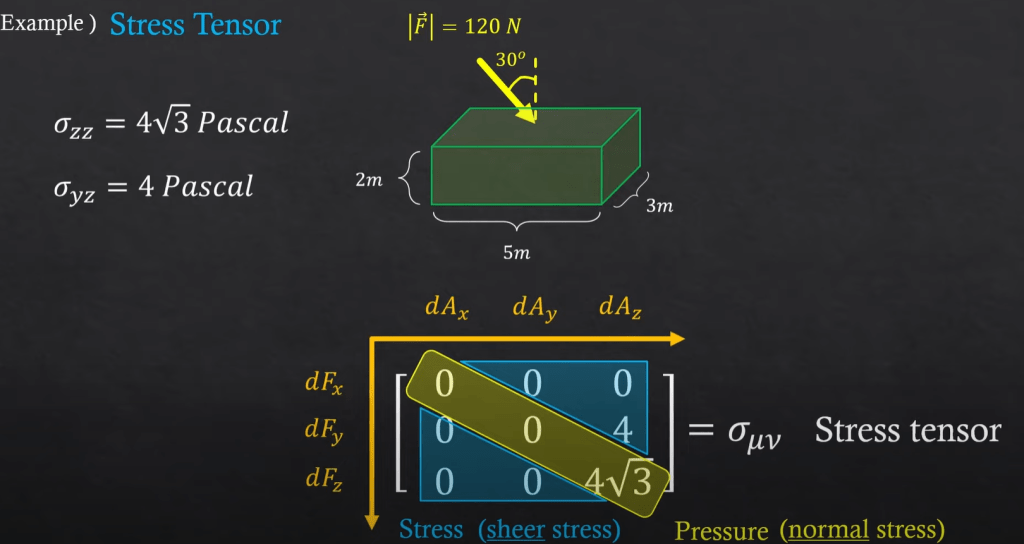
this stress tensor is rank 2 in 3D space.

In General Relativity, which is in 4D space, the row is energy and column is volume, but the division is still in stress unit, hence it’s called Energy-Stree-Tensor

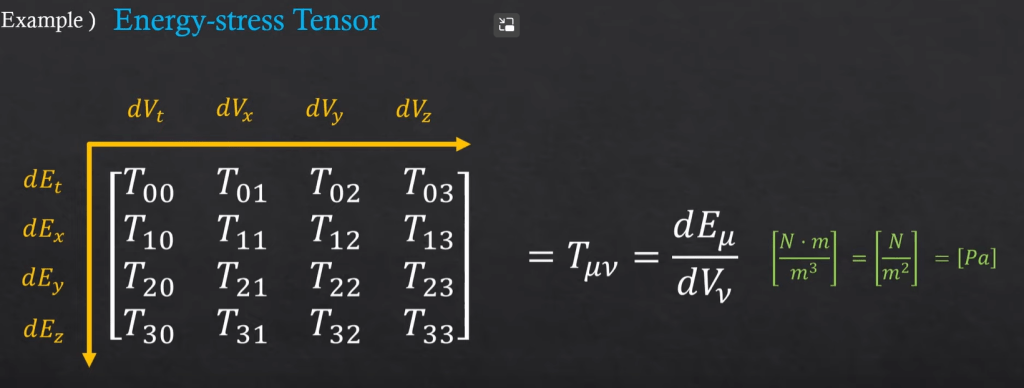
Since E is scalar, so dE is bit puzzling, but we can rewrite it into

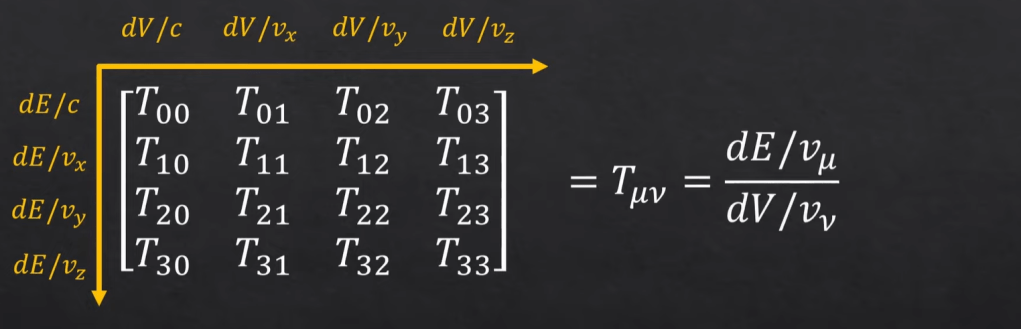
So stress tenso in 3D or 4D as described above are rank-2 tensor, or two physical properties, then it can be written also as

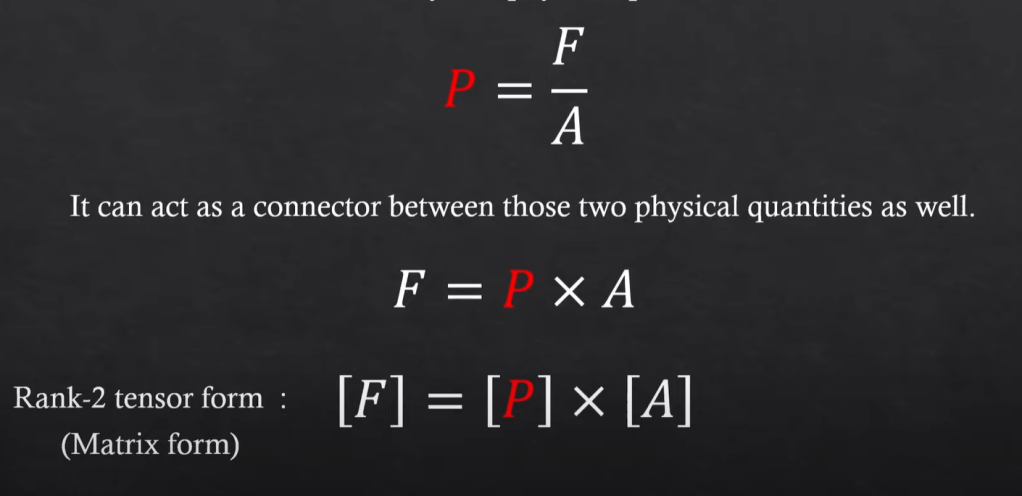
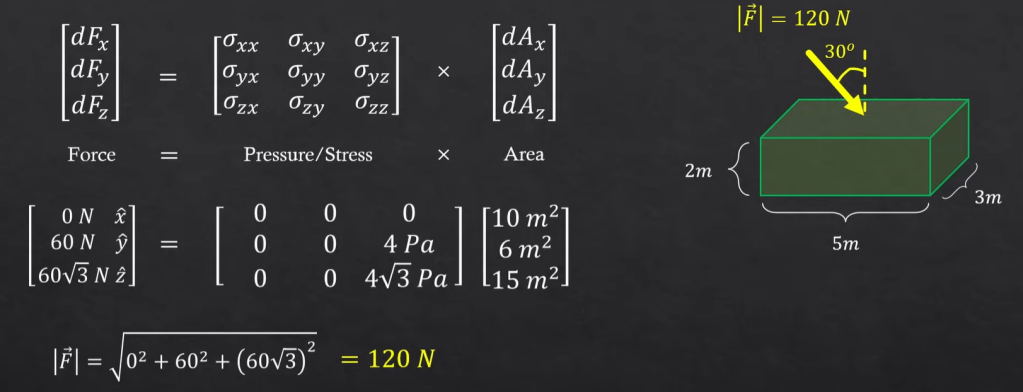
Einstein’s GR equation

Einstein’s field equations essentially tell us: given a distribution of matter and energy (described by the energy-momentum tensor), we can determine how spacetime is curved (described by the Einstein tensor). This curvature of spacetime then dictates how objects move within it, encapsulating the idea that “mass tells spacetime how to curve, and spacetime tells mass how to move.”

“A scalar is a point with only magnitude. A vector is a point with one direction. A tensor is a point that relates multiple directions.”

Summary table

Type	Tensor rank	Intuitive picture	Example
Scalar	0	A point with a value	Temperature, mass
Vector	1	A point with one direction	Velocity, force
Tensor (2nd order)	2	A point relating two directions	Stress, inertia matrix
Tensor (n-th order)	n	A point relating n directions	Curvature in general relativity