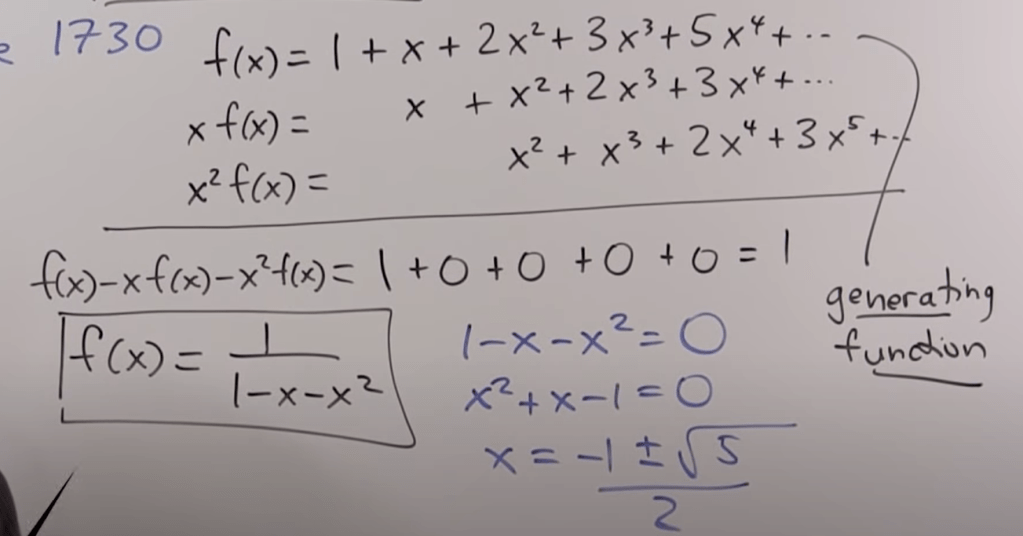A Banach space is a complete normed vector space, meaning that it is equipped with a norm (a way to measure the size of vectors) that satisfies certain properties and that every Cauchy sequence (a sequence of vectors where the distance between any two vectors gets arbitrarily small as you go further along the sequence) converges to a limit in the space. Examples of Banach spaces include spaces of functions (such as continuous functions or square-integrable functions) or spaces of sequences.

A Hilbert space, on the other hand, is a special type of Banach space that is equipped with an inner product (a way to measure the angle between two vectors) that satisfies certain properties. The inner product allows us to define the norm of a vector as the square root of the inner product of the vector with itself. In addition, every Hilbert space is complete, meaning that every Cauchy sequence of vectors converges to a limit in the space.

One of the key differences between Banach spaces and Hilbert spaces is that Hilbert spaces have more structure than Banach spaces. The inner product in a Hilbert space allows us to define notions such as orthogonality and projection that are not available in general Banach spaces. As a result, many of the techniques used in the study of Hilbert spaces, such as orthogonal decomposition and the spectral theorem, are not available in general Banach spaces.

Another difference between Banach spaces and Hilbert spaces is that every finite-dimensional Hilbert space is isomorphic to Euclidean space (i.e., space with the usual inner product), while the same is not true for Banach spaces. In fact, there are many non-isomorphic Banach spaces, while every separable Hilbert space is isomorphic to a certain type of Hilbert space called l2 space.

Spectral theory is the branch of mathematics that studies the properties of operators on a vector space, specifically their spectra, which are the sets of all possible eigenvalues of the operators. Spectral theory is a fundamental part of functional analysis and has numerous applications in physics, engineering, and other areas of mathematics.

The Spectral Theorem is a fundamental theorem in linear algebra that relates to the eigenvectors and eigenvalues of a linear transformation or a matrix. It states that for a self-adjoint linear transformation or matrix, the eigenvectors form an orthonormal basis for the space and the corresponding eigenvalues are real.

The name “spectral” comes from the fact that the theorem is related to the decomposition of a linear transformation or matrix into its spectral components, which can be thought of as the different frequencies or “spectra” of the transformation. The theorem allows us to decompose the linear transformation or matrix into its constituent parts, each of which corresponds to a particular eigenvalue and eigenvector.

Combinatorics is a branch of mathematics that deals with the study of discrete structures, such as finite sets, sequences, graphs, and permutations. Combinatorics is concerned with counting the number of arrangements or combinations of objects, determining properties of these arrangements, and developing methods for constructing and analyzing them.

Combinatorics can be divided into several subfields, including enumerative combinatorics, graph theory, and combinatorial optimization.

Enumerative combinatorics involves counting the number of objects with certain properties. For example, how many ways are there to arrange n distinct objects in a line, or how many ways are there to choose k objects from a set of n objects?

Graph theory is concerned with the study of graphs, which are mathematical objects consisting of vertices (points) and edges (lines connecting pairs of vertices). Graph theory is used to model real-world phenomena, such as social networks, transportation networks, and electrical circuits.

Combinatorial optimization is concerned with finding the best solution to a problem among a finite set of possible solutions. For example, what is the shortest path between two points in a network, or what is the largest subset of a set of objects with a certain property?

Fibonacci sequence can be solved by Combinatorics: