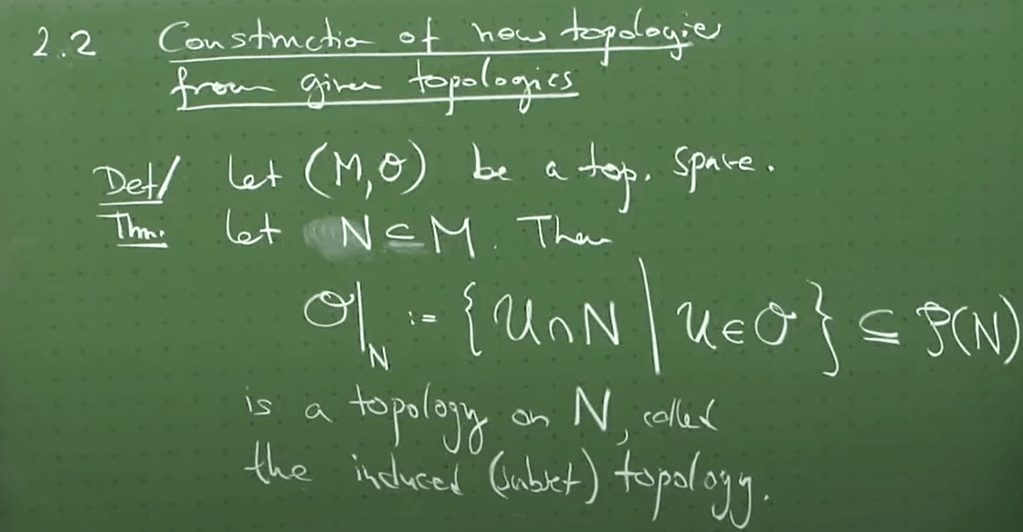Brilliant teacher, his explanation is not easy to follow but concise and accurate, worth to make notes.

A topological space is defined as a set of points, along with a collection of subsets, called open sets, which satisfy certain axioms. These axioms are designed to capture the intuitive notion of nearness or proximity between points in a space, and allow us to define and study concepts such as continuity, convergence, connectedness, and compactness.

here are the axioms that define a topological space:

1. The empty set and the whole space are open: The empty set and the entire space are both considered to be open sets. This ensures that every topological space has at least two open sets.
2. Finite intersections of open sets are open: If you have a collection of open sets in a topological space, their intersection is also an open set. This means that the space remains open when we take the intersection of any finite number of open sets.
3. Arbitrary unions of open sets are open: If you have any collection of open sets, their union is also an open set. This means that the space remains open when we take the union of any number of open sets, even if it is infinite.

These axioms define what is called a “general topology,” which is the most basic and widely studied type of topology. There are other types of topologies, such as metric topology and order topology, that impose additional structure on the space by adding extra conditions to these axioms.

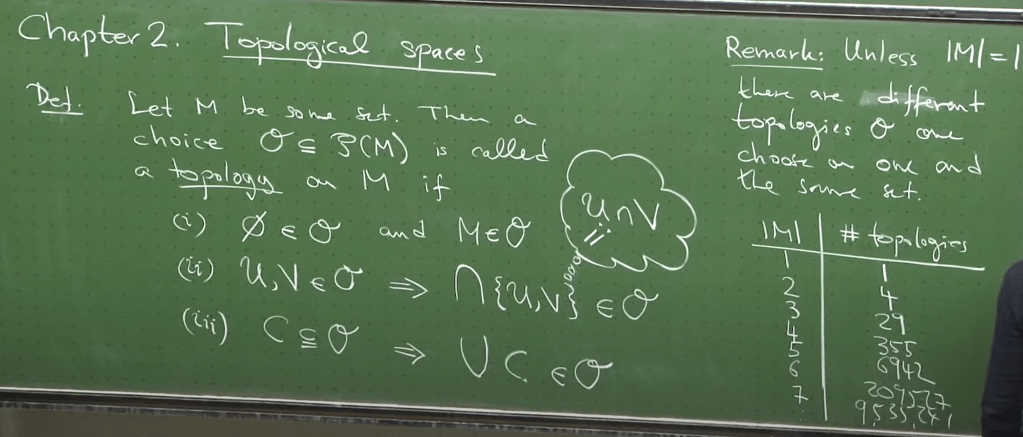
The topology space is defined more rigorously: the pair (M, Q) is called a topological space. M is the set, while Q a choice that belongs to the power set P(M), combining/pairing the two is called topological space.

Examples are discrete topology, chaotic topology and

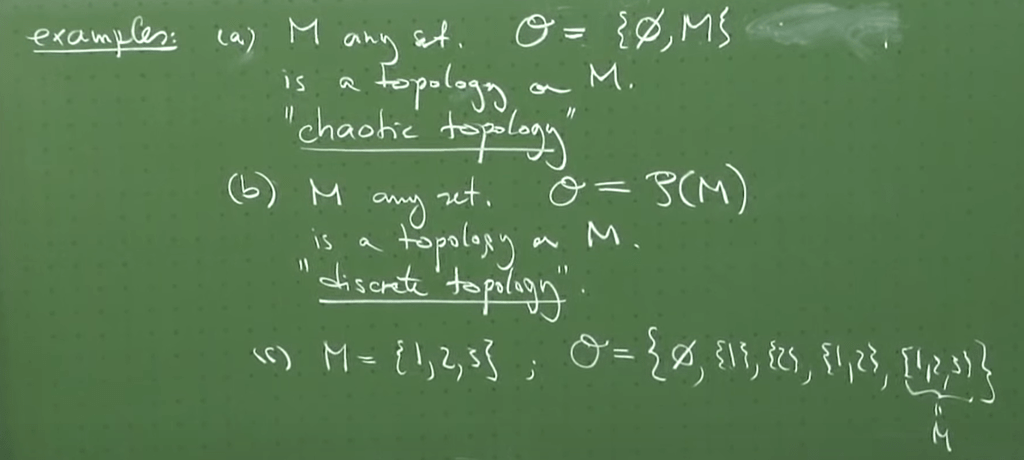
Now define an interesting and also important topological space set

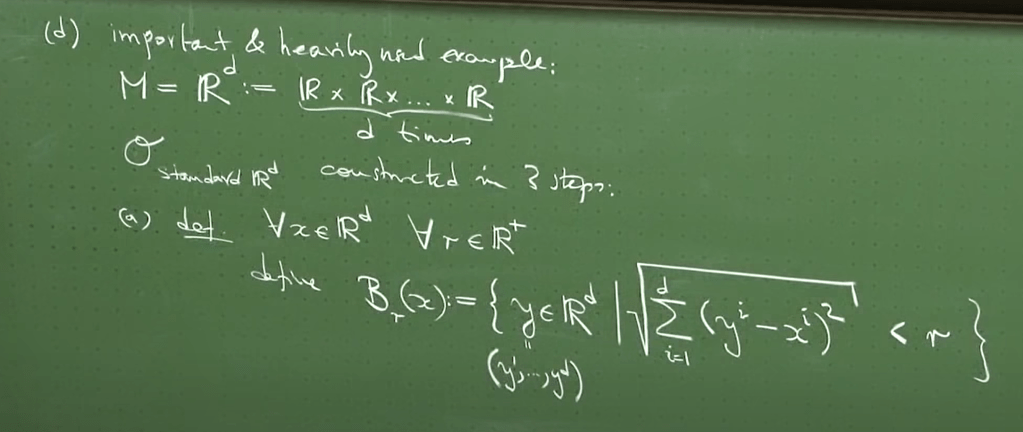
even at the glance it looks complicated we can identify it is the norm 2, or geometrically it is within a ball of radius r around point/center x.

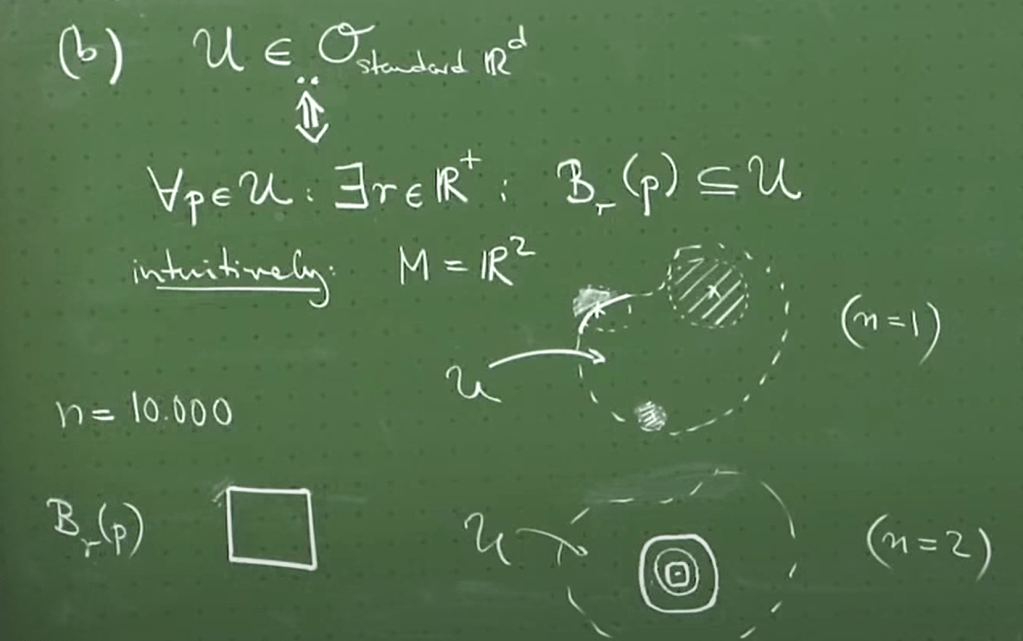
Once can construct a new topology from a given topology.