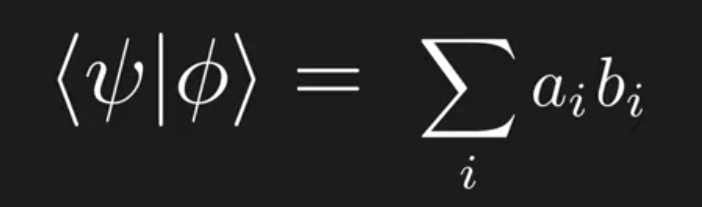Find a proper math framework using math language to describe physics is the key. For example, particles are represented by vectors (later on it’s worth further scrutinized if proper) and energy etc. are represented by operators. Note math summarization is based on structure and pattern not by concrete objects that most of us stuck to.

First, to study vectors, we define vector space first, the abstract form that we’re always being told are:

So quantum state is like a particle, being represented by vector and uniquely notated as \( \psi \). Next to express the properties such as position, which is not discrete but continuous, integral is to be brought in equivalent to summation sign.

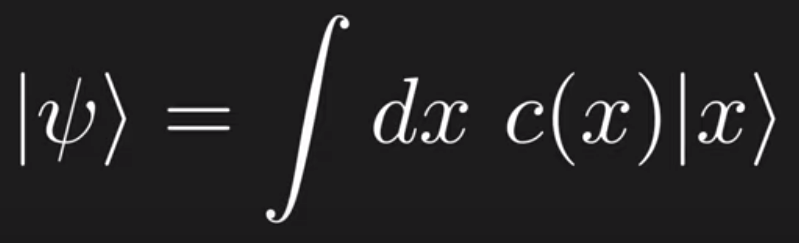
in comparison to below one can see intuitively how taking integral is exact upgrade from discrete summation.

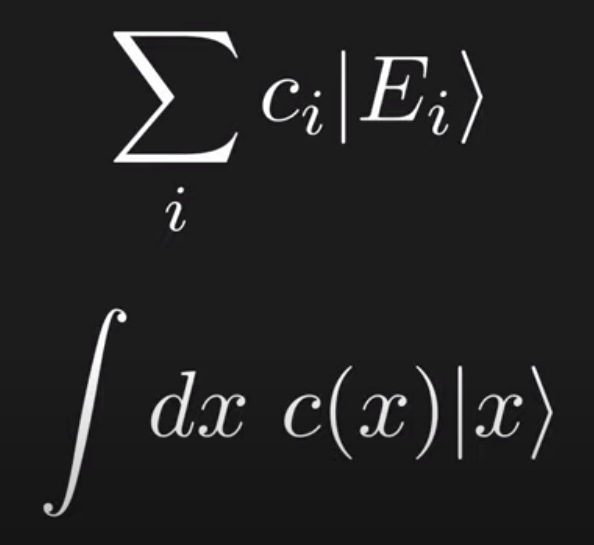
The dxc(x) is the coefficient ci, which is also interpreted as probability, later on we replace c(x) with the position wave function psi(x), not as a normal function f(x). Yes, wave function is a vector, but it’s actually represent the coefficient.

To overcome the issue of infinity in vector space, we have to make it stricter by using Hilbert space, where it’s equipped with an inner product that is Cauchy complete. See how important inner product is? it’s right in the definition of Hilbert Space, and to understand inner, we need to know dot product, especially how dot product is invented by mathematicians. Note when we flip ksi and psi, we need to add the left part/ket a conjugated sign.

The power of using inner product together with finding the orthonormal basis/eigen vectors to psi and phi, it’s easy to reason below and not only the computation is feasible and easy, and wow, it’s exactly the dot product.