Why physicists use commutator, it has practical reason to make QM computation easier:

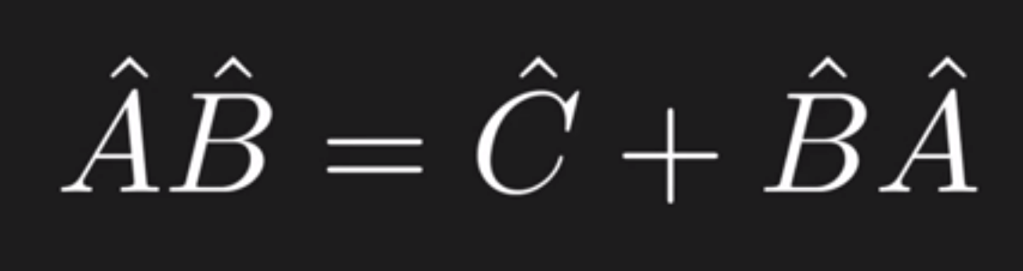
Here is the most fundamental insight from Brandon: if A and B commute,

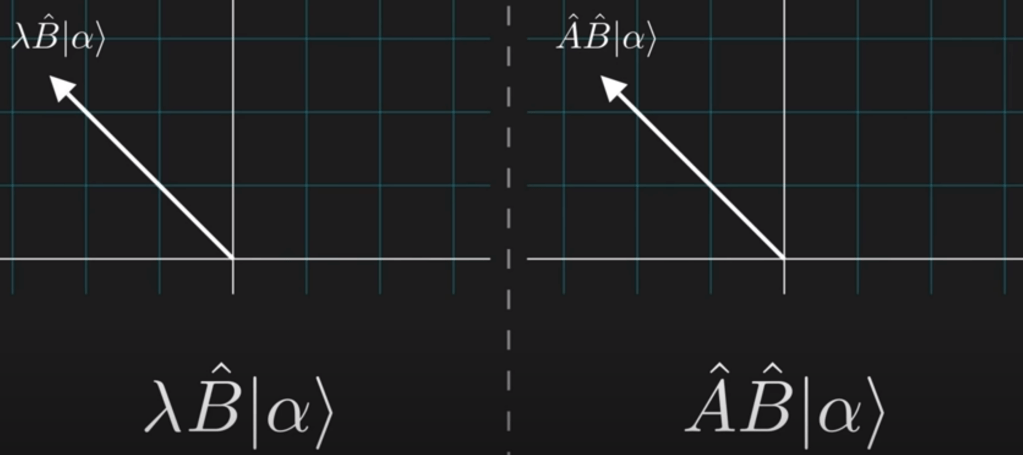
non-degenerate eigenvector of A must also be eigenvector of B.

If two operator A and B commute, they share simultaneous eigenbasis:

Conversely, if A and B do not Commute, we can prove that they do not share a simultaneous eigen basis. And this is the essence of Heisenberg uncertainty principle that you can not measure momentum and energy at the same time because if one is collapsed, say P, the other one E is still formed of linear combination of various eigen states.

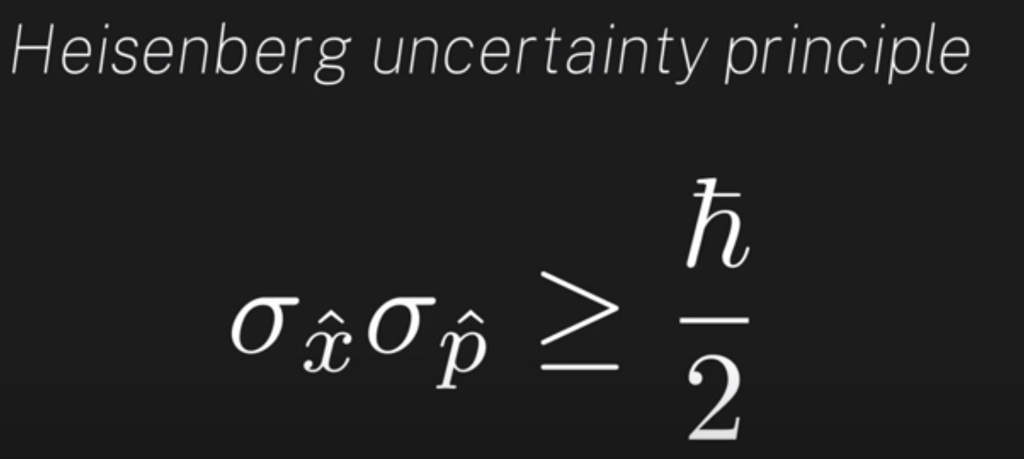
The momentum and position operators do not commute, and therefore they do not share a simultaneous eigenbasis.

This non-commutativity is at the heart of the Heisenberg uncertainty principle, which states that it is impossible to simultaneously measure both the position and momentum of a particle with infinite precision. The more precisely one of these quantities is known, the less precisely the other can be known. This is a fundamental limitation of quantum mechanics and is not due to any limitations in the measuring instruments. If you measure momentum, the position is residing in the space where it’s an aggregation of infinite probabilities of position eigen states, vice versa.

Next, dig into the Unitary Operator, another very important operator other than Hermitian operator. It’s intuitive to think some operator/transformer a pair of vectors retaining the angle and length is rotational operator. But is it same as Unitary operator?

we found all the eigenvalues are unit 1

Why it’s so important because it preserves the probability in QM, probabilities are what we measure!