Continue, but quite marveled at the beauty and simplicity of viewing special relativity using group/transformation in three rotations and three boosts, all derived from invariance –> from g = diag(-1, 1, 1, 1) to find these transformations.

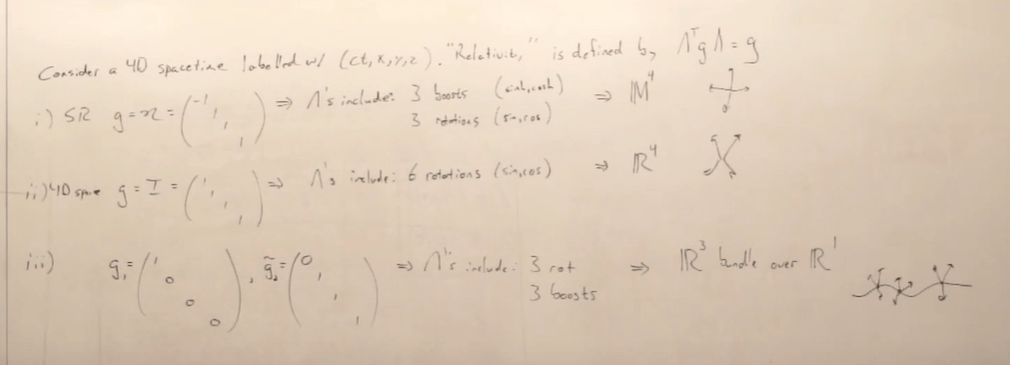
The third scenario, R3 bundled over R1, is the Galileo Special Relativity.

SO(1, 3) is the proper Orthogonal Lorentz group.

Was back on the 2019 General Relativity series no.8 on moving from 3D to 4D relativistic perspective to solve kinematics and dynamics. There are two major problems, one is what monadically changing denominator t to be replaced, which is tou. The other is the weird thing of the velocity v–> U miu:

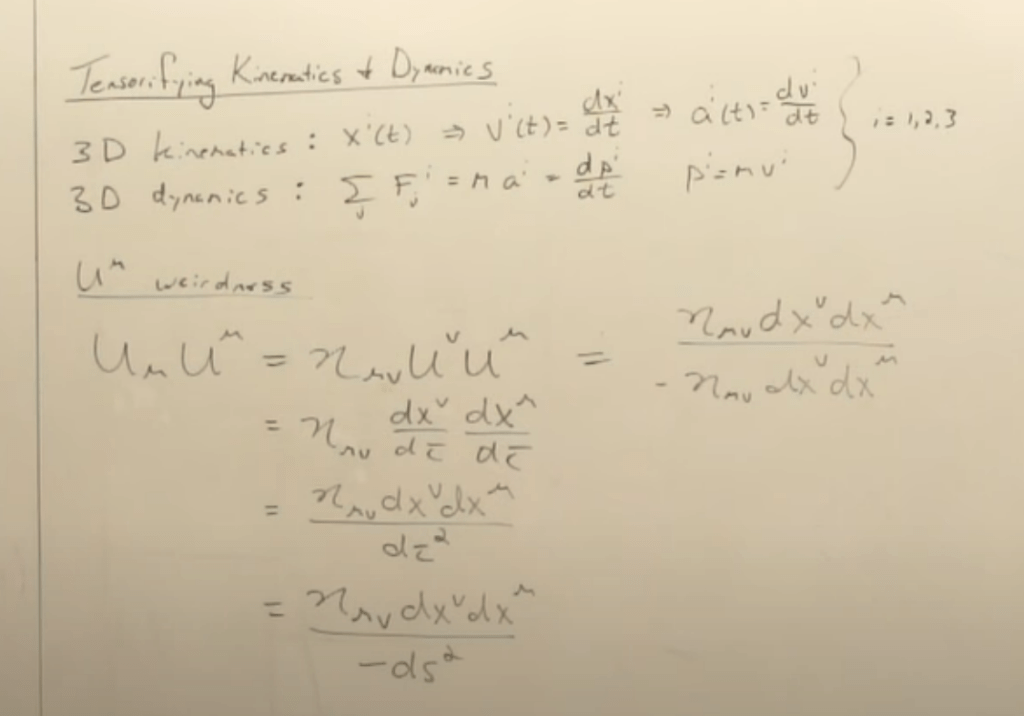
So it’s weird that the velocity squared is -1. We need to be mindful that the equation breaks when the points moves at the speed of light, because ds^2 = 0, meaning in 4-D spacetime, an object traveling at speed of light has zero length traveled.

it’s actually totally correct to have above equation = -1 because we use dtou, or d length of distance as the denominator instead of time t, if we apply same spirit in 3D, we will find their velocity square = 1:

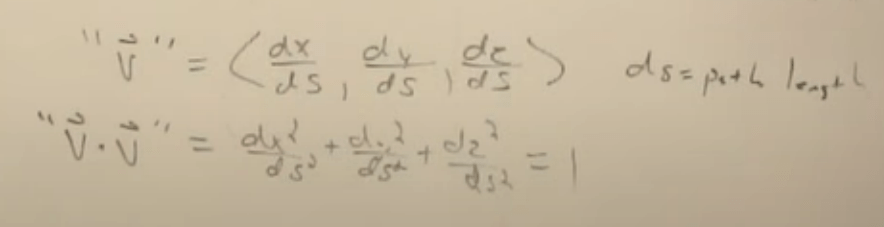
Now imaging you are in a frame of S and there is a point at rest you are observing, let’s put it to 4D spacetime and formulate it:

Then Einstein has to continue on exploring the momentum: