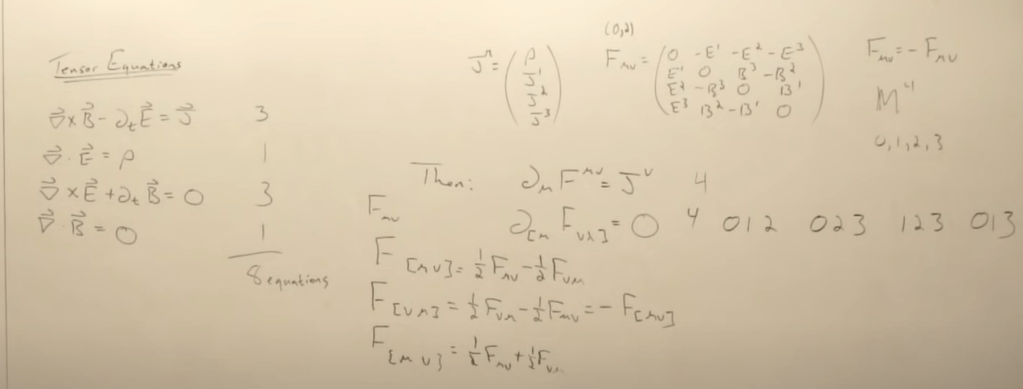What is tensor, the metric is a (0, 2) covector space tensor, its inverse (2, 0) is tensor living in vector space. Note Einstein diag(-1, 1, 1, 1) happens to have the metric and inverse metric identical, but you can regard them as tensor and inverse tensor separately.

Higher-order tensors have three or more indices and can be visualized as multi-dimensional arrays. For example, a 3rd-order tensor can be thought of as a “cube” of numbers, where each element is specified by three indices. It’s multi-linear map that transform objects in space of vector or/and covector/dual vector to real. Or, informally, a tensor is anything transforms like a tensor, so how they transform, the rules are:

Note the tensor miu niu is defined as T miu prime, niu prime = two matrices lambda transform sequentially to upper corer(contravariant) on T miu niu. It is essential to tell if some objects are tensor or not, it’s the hard-core step in getting to General Relativity, as what we’ll learn later on the lynchpin in learning Gauge Theory too.

Justing saying matrix loses information on upper and bottom right corner notation info, about if it’s in vector space or dual vector space. It’s important to pay attention to notations in higher level math-tensor,

Note if miu prime is upper, if down it’s inverse

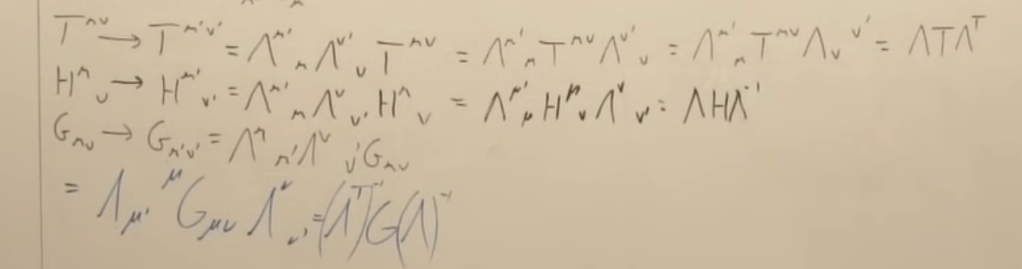
need practicing.

As mentioned, metric tensor is a special kind of tensor, that is symmetrical. Metric tensor also turns a vector to its dual vector, important! conversely, inverse metric tensor takes the dual vector into its corresponding vector.

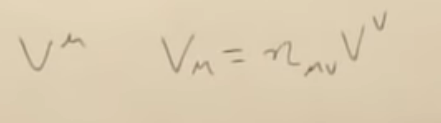
Now moving onto the key concept coordinate x miu in spacetime, x miu transform like a vector but it’s not a vector, delta x miu is a vector, because just stating x miu does not have the length associated.

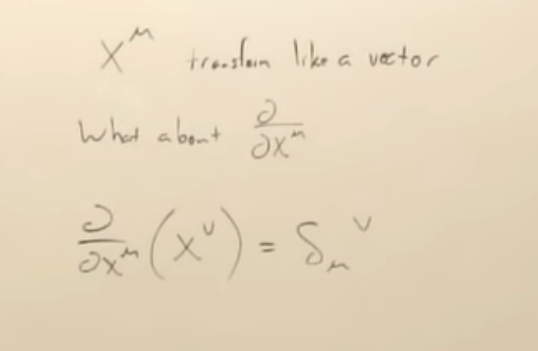
Because delta miu niu in the right side is an invariant, on the left side, x miu transforms like a vector, hence the derivative of coordinate is like a “dual vector”, notation wise, they actually make it

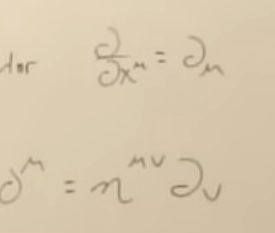
Tensor equations showing for future: