A complex manifold is a generalization of the more familiar concept of a manifold, but with structures that respect complex numbers. Let’s break this down step by step:

1. Manifold: At a basic level, a manifold is a topological space that locally resembles Euclidean space. An example of a 2-dimensional manifold is the surface of a sphere, which locally (if you zoom in on a small patch) looks like a flat plane.
2. Complex Structure: Now, imagine that instead of coordinates that take real values (as is the case for the plane or the surface of a sphere), the coordinates take complex values. This complex structure essentially means that the tangent spaces to the manifold are complex vector spaces, and the transition functions between coordinate charts are holomorphic (complex differentiable).
3. Complex Manifold: Putting the above ideas together, a complex manifold is a manifold equipped with a complex structure. This means that locally, it looks like ��Cn (the complex coordinate space of �n dimensions), and the transition maps between coordinate patches are holomorphic functions.

For a function to be holomorphic on a complex manifold, it needs to be complex differentiable in the manifold’s complex coordinate charts.

Some key points about complex manifolds:

• They are central objects of study in several areas of mathematics, including complex geometry, several complex variables, and algebraic geometry.
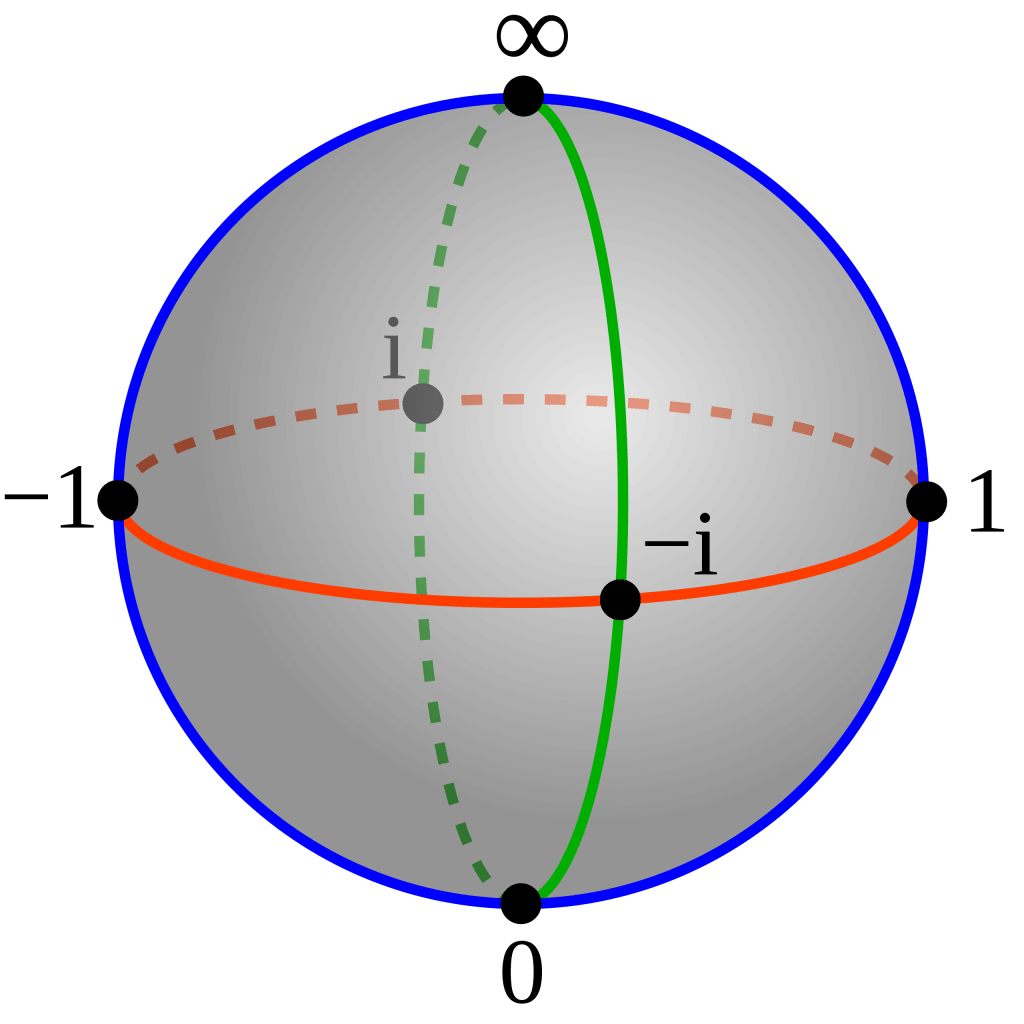
• A classic example of a 1-dimensional complex manifold is the Riemann sphere, which compactifies the complex plane by adding a point at infinity.
• Complex manifolds also play roles in theoretical physics, especially in string theory, where certain types of complex manifolds (like Calabi-Yau manifolds) are of particular interest.

The Riemann Sphere