First, I’d like to jump to Jacobi Method in solving linear system problem.

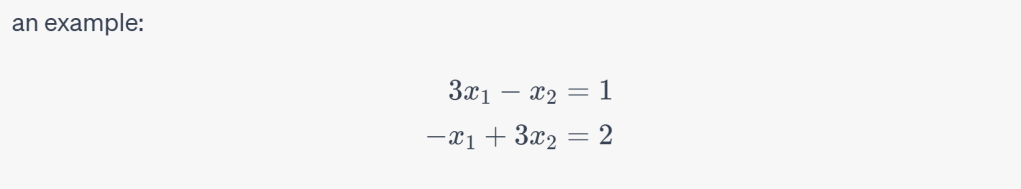
import numpy as np

def jacobi_method(A, b, max_iterations=100, tolerance=1e-10):
    # Split A into D and R
    D = np.diag(np.diag(A))
    R = A - D
    
    # Initialize the solution vector with zeros
    x = np.zeros_like(b)
    for i in range(max_iterations):
        # Calculate the new guess
        x_new = np.linalg.inv(D).dot(b - R.dot(x))
        
        # Check for convergence
        if np.linalg.norm(x_new - x) < tolerance:
            return x_new, i  # Return the solution and number of iterations
        
        x = x_new

    return x, max_iterations

# Define the system
A = np.array([[3, -1], [-1, 3]])
b = np.array([1, 2])

# Solve using Jacobi method
solution, iterations = jacobi_method(A, b)
solution, iterations