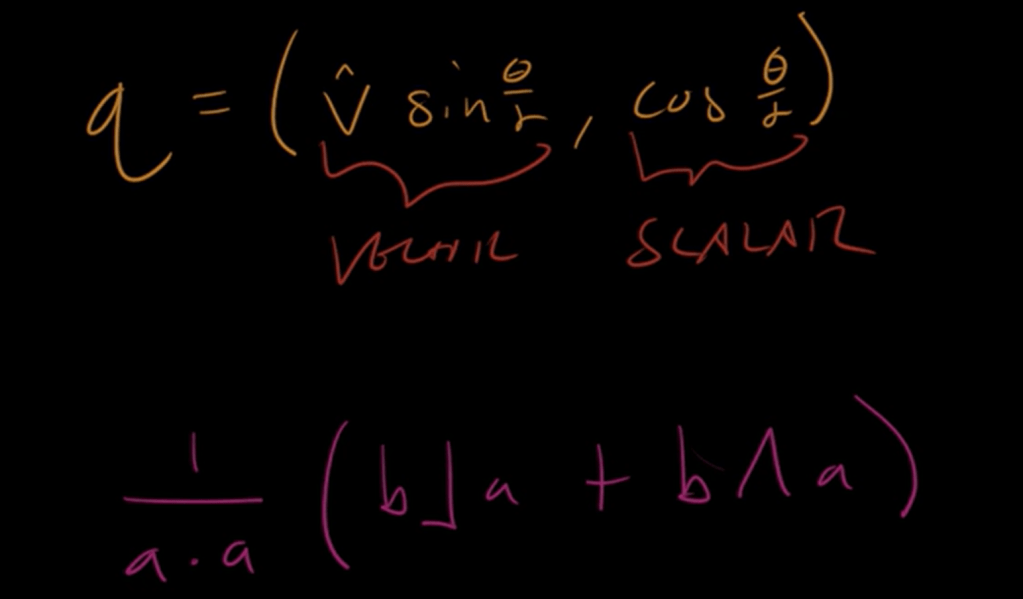Already know edge product etc, what’s new the contraction product

what if both a and b are vectors,

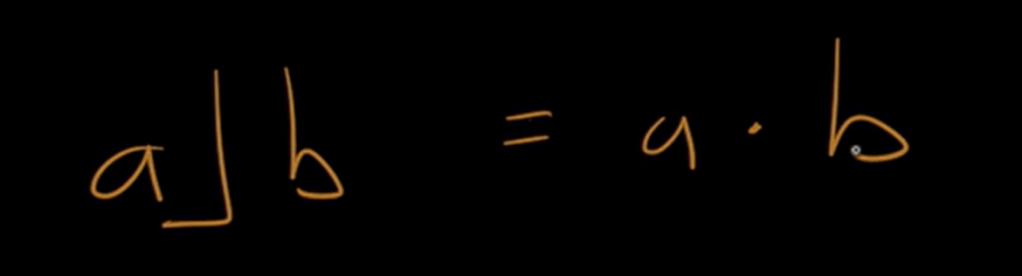
for trivector

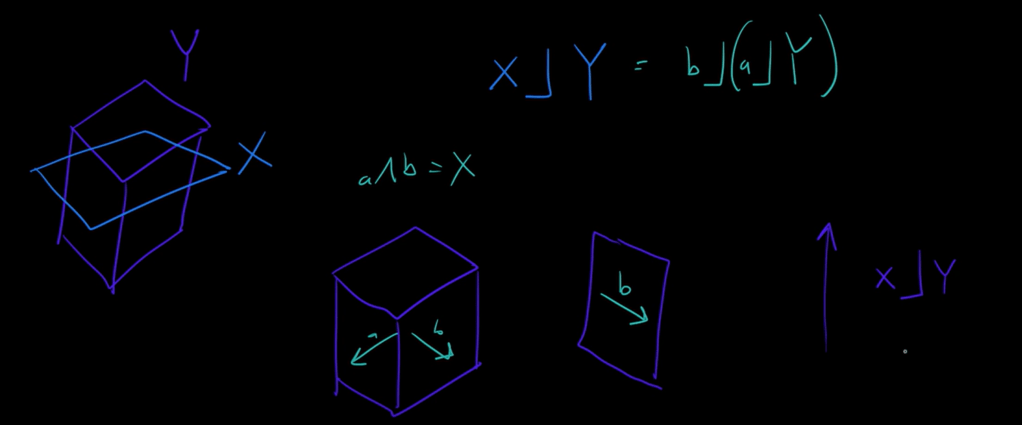
Two vectors can be divided in geometric algebra:

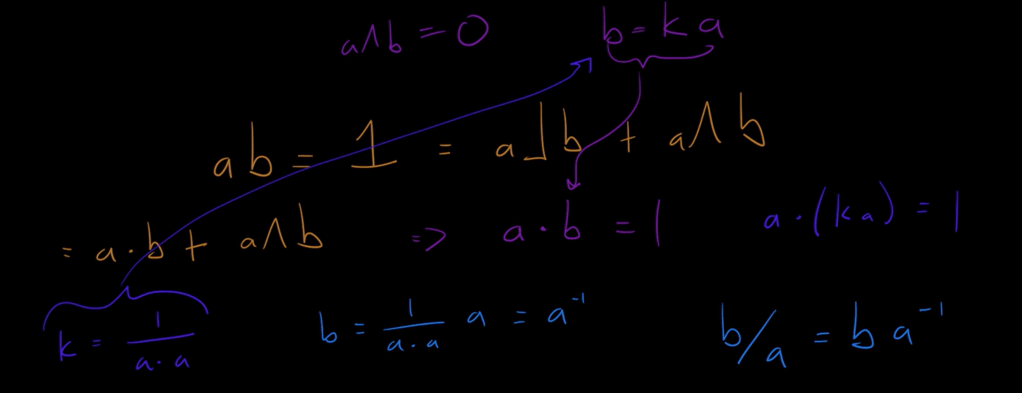
Projecting x on a can be expressed in geometric algebra differently:

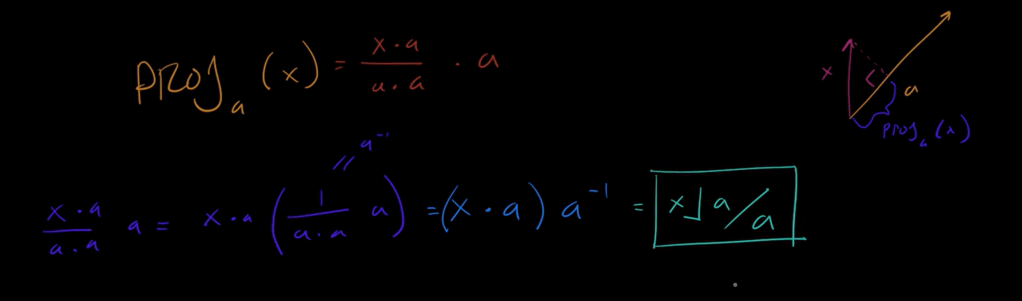
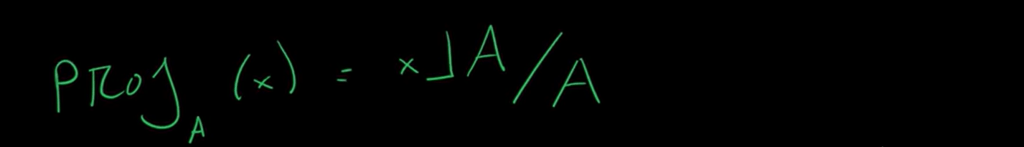
There is projection, and rejection, reflection and rotation, all can be expressed geometric algebraically:

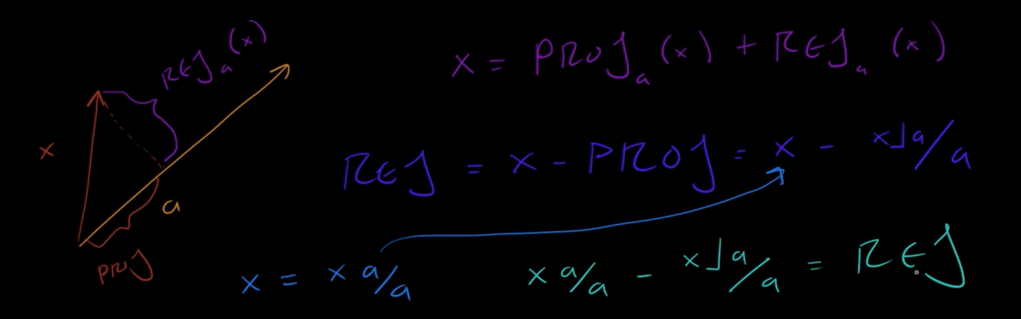
It’s straightforward to see reflection = projection – rejection, leading to the climax of sandwich product, which leads to a clever way to do rotation: twice reflection

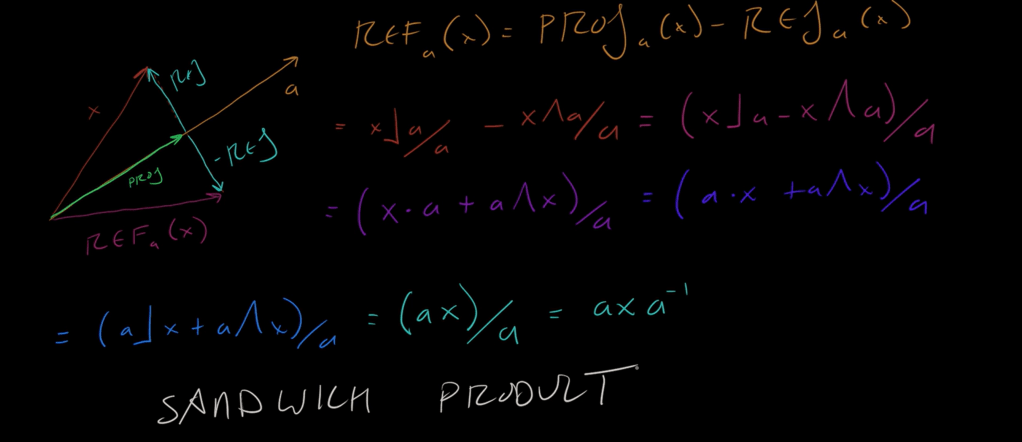
Define or call b/a as a rotor,

Quaternion is just a rotor, rotating by double the angle.

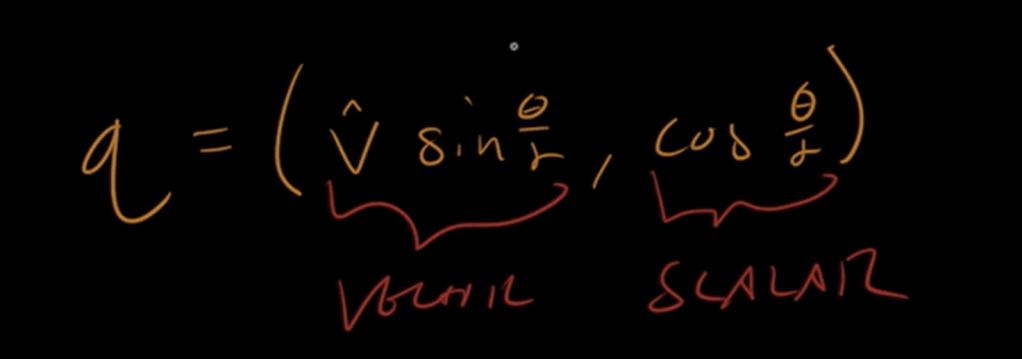
So the identification or correspondence between quarternion and geometric algebra