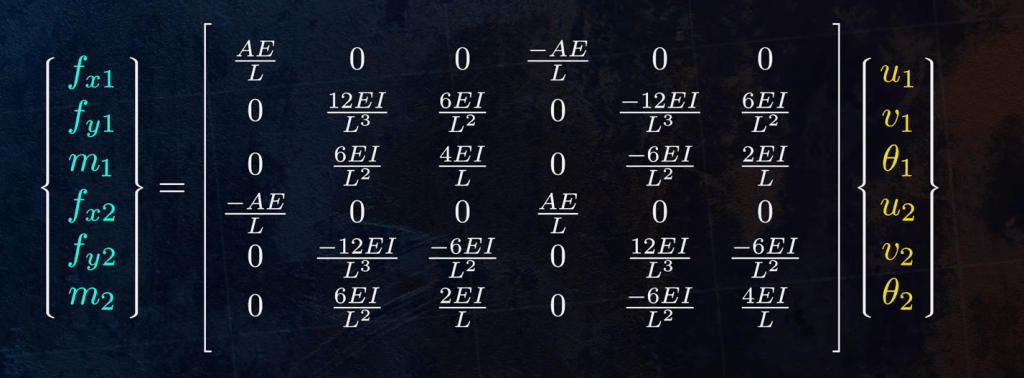The essence of FEM is to reduce complex formula to individual Ax=b by dividing an object into discretional meshes bounded by nodes, then each node can be defined by matrix.

For example, Assume a simple 1D rod divided into two elements, the Stiffness matrix (assuming same material and cross-section, and unit length for simplicity) is A = np.array([[2, -1, 0], [-1, 2, -1], [0, -1, 1]]), then Load vector (assuming some arbitrary loads) b = np.array([1, 0, 0]), then Solving Ax = b for x (displacements) x = np.linalg.solve(A, b)

in this efficientengineer video, more color is given:

how to mathematically describe:

for this two elements, the math description is as follows, knowing f is the force, k matrix for stiffness matrix denoting every stiffness coefficient in hook’s law, and {u} in 6 dimensions is the displacement vector.