Lie theory and the concept of the Poisson bracket are deeply intertwined in the study of mathematical physics and differential geometry. Here’s a brief overview of their relationship:

1. Lie Algebras: At the heart of Lie theory is the concept of a Lie algebra, which is a vector space equipped with a binary operation called the Lie bracket that satisfies certain axioms. These axioms ensure that the Lie bracket captures the essence of the commutator of matrices or operators.
2. Poisson Manifolds: A Poisson manifold is a smooth manifold equipped with a Poisson bracket operation, which is a binary operation on the space of smooth functions on the manifold. This Poisson bracket generalizes the canonical Poisson bracket from classical mechanics and satisfies axioms similar to those of a Lie bracket.
3. Relationship: On a Poisson manifold, the Poisson bracket defines a Lie algebra structure on the space of smooth functions. This is because the Poisson bracket of two smooth functions is again a smooth function, and the bracket satisfies the axioms of a Lie bracket.

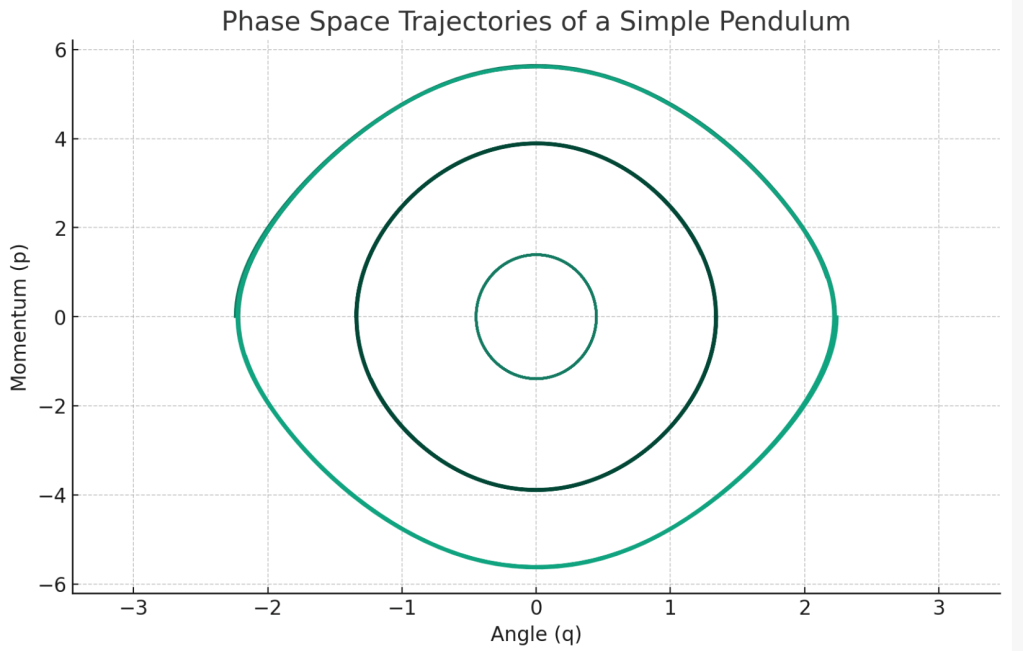
This blog 01 is more general, i will follow Elliot’s series to go on. But First, curious to know how Hamiltonian flow depict a pendulum vividly?