First, to be truly clear of the math definition before reaching the fundamental theorem of geometric calculus.

The key is to think of delta F as a geometric product, given operator of gradient can be treated as a scalar:

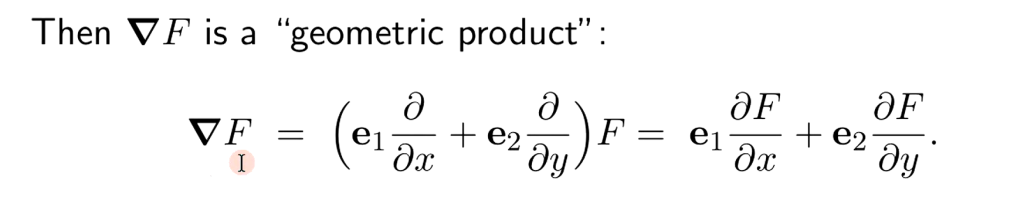
Let’s say F is a multivector valued function on an open set in R2, the operator delta is invertible, F is on the boundary of the set U.

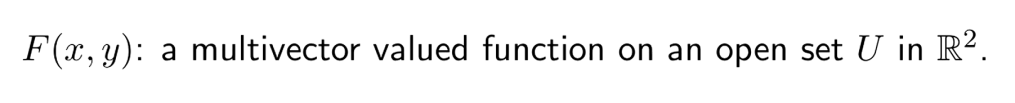
Now Maxwell’s equation can be succinctly expressed in geometric calculus form

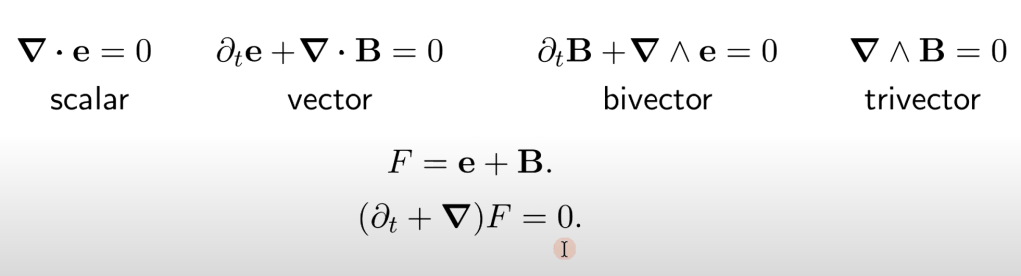
Alan then introduced the concept of reciprocal basis as follows:

It’s worthy to note the difference between reciprocal and dual basis:

Finally define tangent space basis:

Note the reciprocal basis is used instead to ensure the orthogonality.