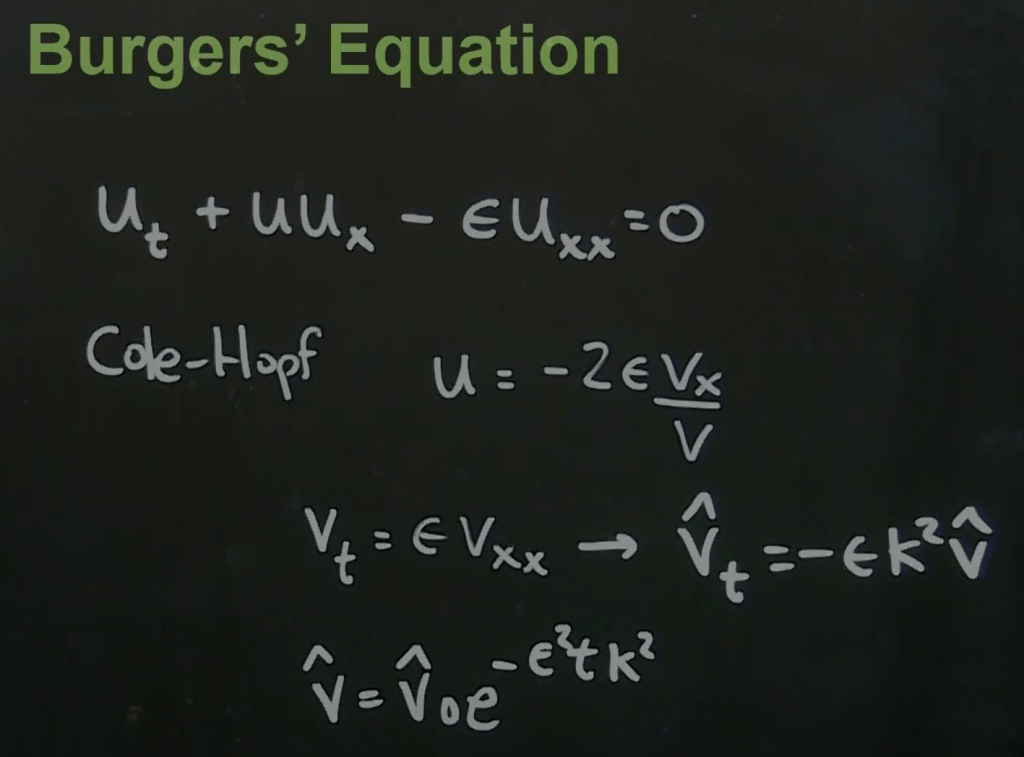The Koopman operator is a mathematical concept used in the field of dynamical systems and control theory. It is named after the American mathematician Bernard O. Koopman, who introduced it in the 1930s. The Koopman operator plays a significant role in the analysis of nonlinear dynamical systems, particularly in the study of chaotic systems and data-driven modeling.

In simple terms, the Koopman operator is a linear operator that acts on functions of the state variables of a dynamical system. It provides a way to transform the evolution of a nonlinear system into a linear problem in a higher-dimensional space, often referred to as the “Koopman space” or “observables space.”

Mathematically, if you have a dynamical system described by a set of differential equations like: dx/dt = f(x), Where x represents the state vector of the system and f(x) is a nonlinear vector field, the Koopman operator K is defined as an operator that maps a function g(x) to another function G(y) as follows: G(y)=Kg.

One of the key advantages of using the Koopman operator is that it can sometimes simplify the analysis of complex nonlinear systems by linearizing the dynamics. This linearization can make it easier to study stability properties, control systems, and other aspects of the system’s behavior.

For example,

The applicaiton is profound, such as wave equations with different level of complexity:

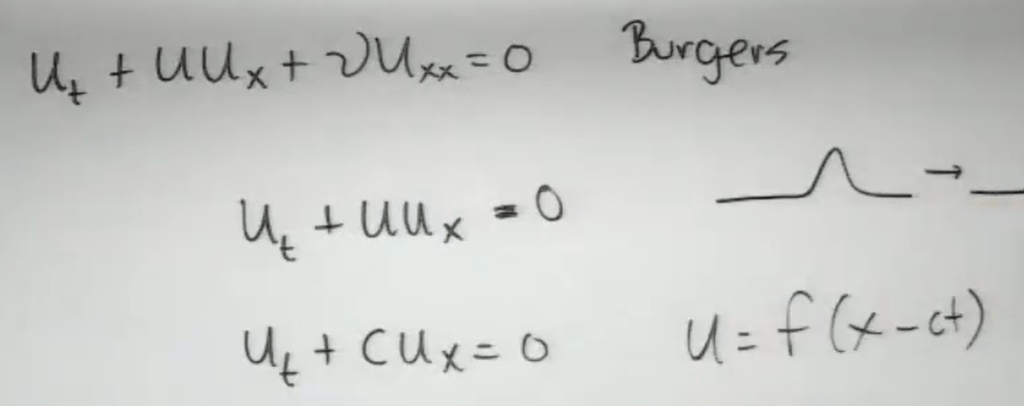
Let’s see how it is applied in solving PDEs and relationship between DMD (dynamic mode decomposition) and Koopman operator. DMD and Koopman operators relationship can be illustrated by below diagram by Nathan Kutz:

Very rarely we can turn a nonlinear manifold on the left to the flat space in the right, such as the example

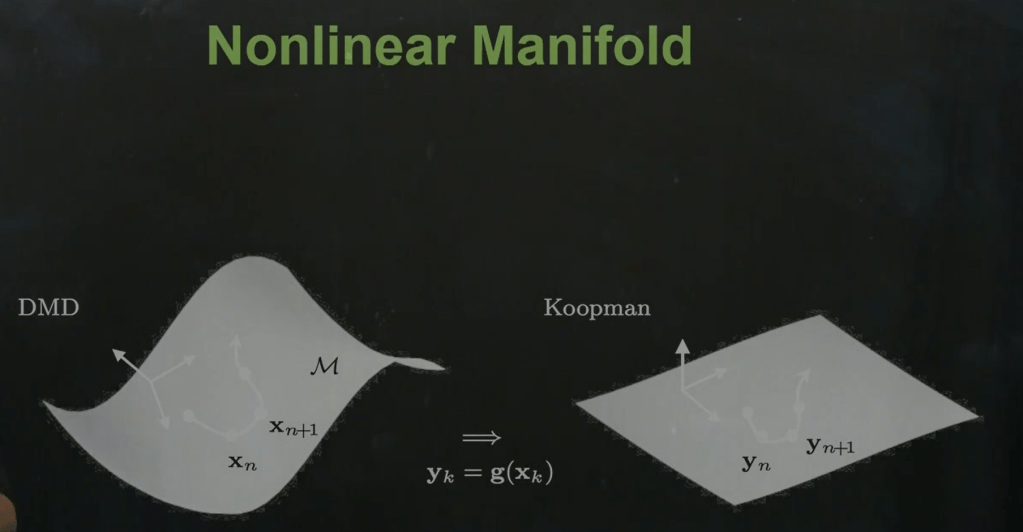
But we can make it weakly non-linear and then apply perturbation theory to deal with/compute.

A practical example is to solve Burger’s Equation by Vt = Vxx conversion.