What is bifurcation theory? It focuses on the study of sudden changes in the behavior or structure of solutions to a system of equations as a parameter within that system is varied. These changes are known as bifurcations and occur at specific values of the parameter, called bifurcation points.

Types of Bifurcations: There are several types of bifurcations that are typically studied:

• Saddle-Node Bifurcation: This occurs when two equilibrium points of a system (one stable and one unstable) merge and annihilate each other as a parameter is varied.
• Transcritical and Pitchfork Bifurcation: These involve changes in the stability and number of equilibrium points. In transcritical bifurcation, two equilibria exchange stability; in pitchfork bifurcation, a single equilibrium point splits into multiple equilibria.
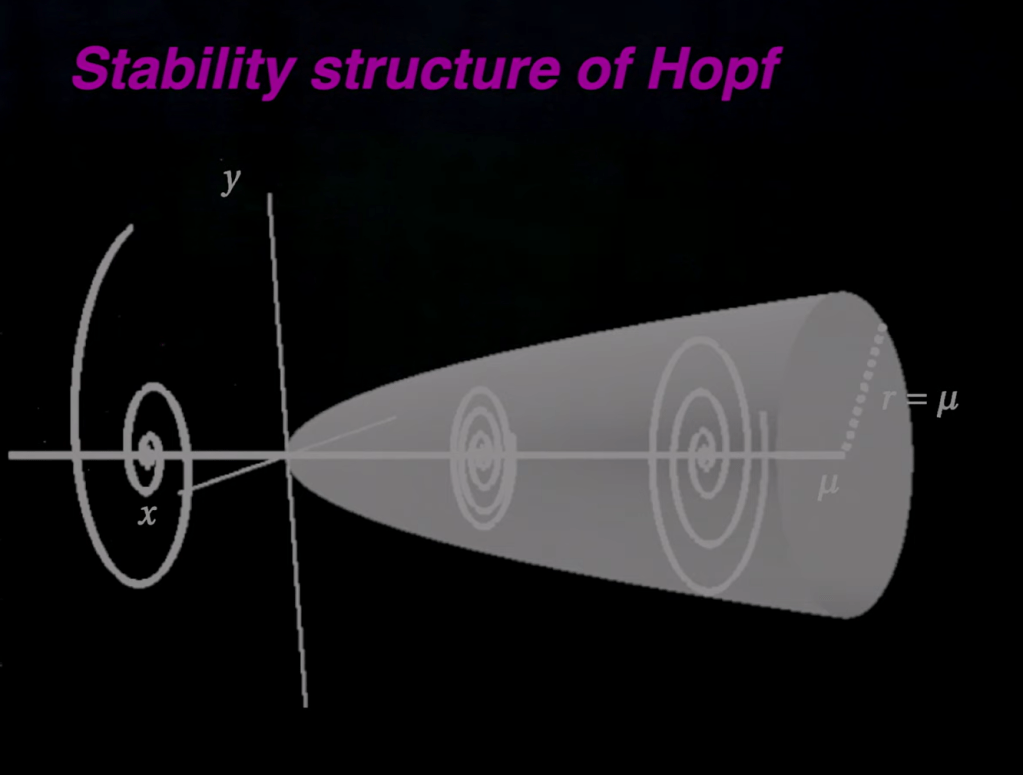
• Hopf Bifurcation: This type occurs when an equilibrium point of a system loses stability and a periodic solution (like a limit cycle) emerges.

Analyzing stability and changes in stability is a crucial part of bifurcation theory. This often involves examining the eigenvalues of the Jacobian matrix of a dynamical system at equilibrium points.

Look at an example by Nathan Kutz

the key is to find the equilibrium x0 dependent on the parameter mu. x0 is where the change is zero, hence equillibrium.

then apply perturbation theory aournd x0:

here the sign of x0 is critical in terms of its solution will blow up or converge to infinitely small, the diagram of x and mu is

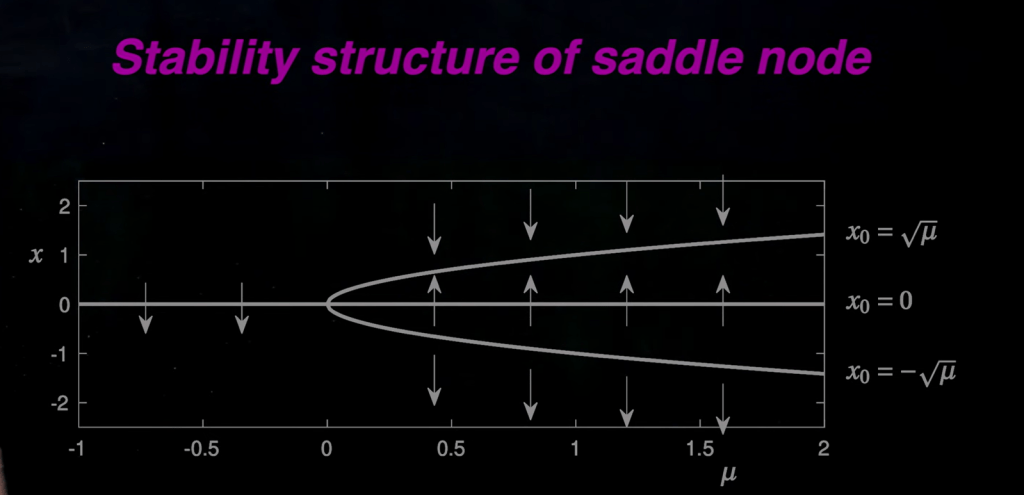
It’s bit mind twisting to look at the fork point and figure out how the solution in upper side converge, while bottom diverge.

Now let’s look at the transcritical bifurcation: there are two equlibrium points, x0 = 0 and x0 = mu

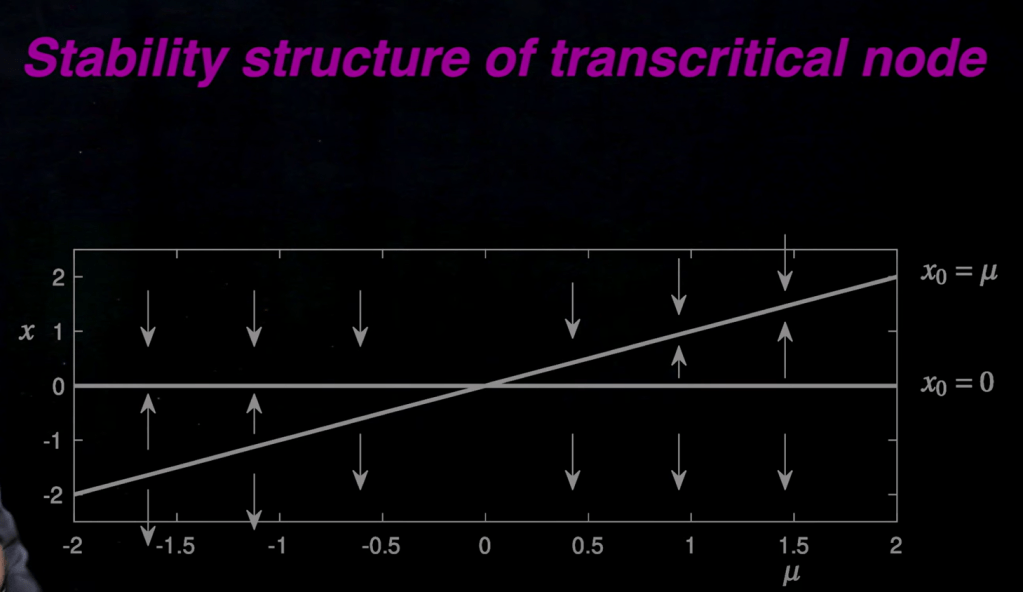
you can see above, why this is called transcritical, because the bifurcation point jumped.

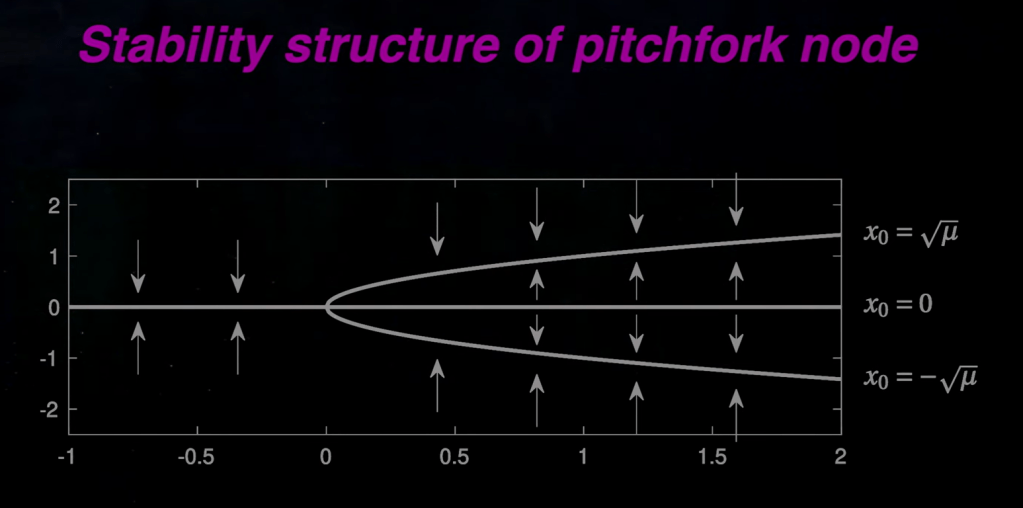
Third, pitchfork bifurcation

Lastly Hopf bifurcation