The development for the non-abelian case of the strong interactions will follow a very similar path as the abelian case of electromagnetism. The symmetry is based on SU(3) acting in a three-dimensional space with eight generators instead of U(1) acting in a one-dimensional space with one generator. Because all matter consists of spin- 1 2 particles, Quantum Chromodynamics will at least be partly described by a spinor field Ψ with four components in spin space but in addition with the three components Ψr, Ψb, Ψg in color space. Color space with the three colors red, blue, green as a basis is three-dimensional and has nothing to do with the spin space which is four-dimensional. One way to keep them separate is that the four components of the spinor are affected but not the three color components if one does a Lorentz transformation, and if one does an SU(3) transformation the three color components are affected but not the four spinor components. Spaces such as the color space are often called iso-spaces or internal vector spaces just to make sure one is not confused between those vector spaces and the vector spaces more related to spacetime.

Transformations of SU(3) act on the vectors with the three color components. Each of the three components Ψr, Ψb, Ψg is a four-component spinor. The strong interaction only acts on the six flavors of quarks which are the up u and down d, the charm c and strange s, and the top t and bottom b quark. red, blue, green as a kind of charge are not three values of the same charge like +e and −e for the electrical charge, but are three distinct types of charge each with two values r, ¯r or b, ¯b or g, ¯g. But in nature one never finds single quarks but only bound states of quarks and only bound states of quarks which are colorless.

Quantum Chromodynamics describing the strong interactions is understood as a theory of local SU(3) invariance acting on quarks only.

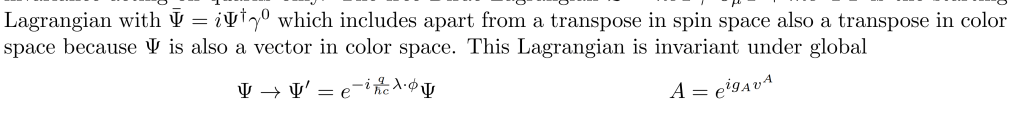
Because SU(3) is the related group of transformations, λ have to be 3 × 3 matrices and thus needs two indices i and j, but because there are eight of them, the index a is needed. This is a generalization of the case U(1) to the non-abelian group SU(3) with multiple generators.
In the next step, the global symmetry is turned into the local one

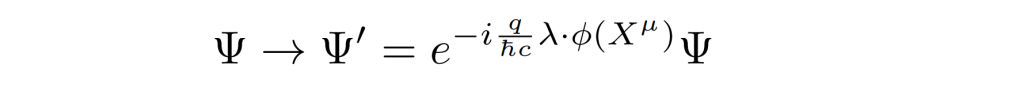
with φ = φ(Xµ). The Lagrangian is no longer invariant under local SU(3), but with the covariant
derivative Dµ = ∂µ + ig λ · Aµ instead of ∂µ similar to the case in electromagnetism one can make
the Lagrangian invariant under local SU(3).