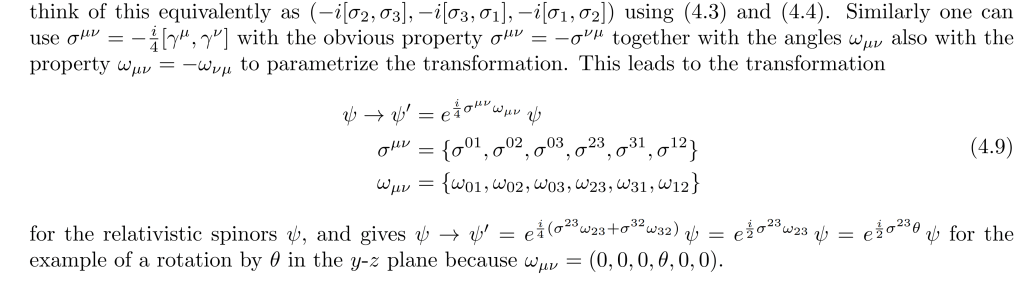The more I learn math and appreciate its power in solving real-world problems, making our modern life seem like magic to our ancestors, the more I realize that the essence of math lies in the ability of mathematicians and physicists to create a system of symbols to describe chaotic phenomena such as heat and light. Bit by bit, they build mathematical frameworks that can interpret, compute, and predict these phenomena through equations and derivations.

For example, you may think of the below math definition of topology, topological space and homomorphism is daunting,

But if we trace back from the very early time, when geometry mathematicians are studying point, lines:

First line can be expressed algebraically

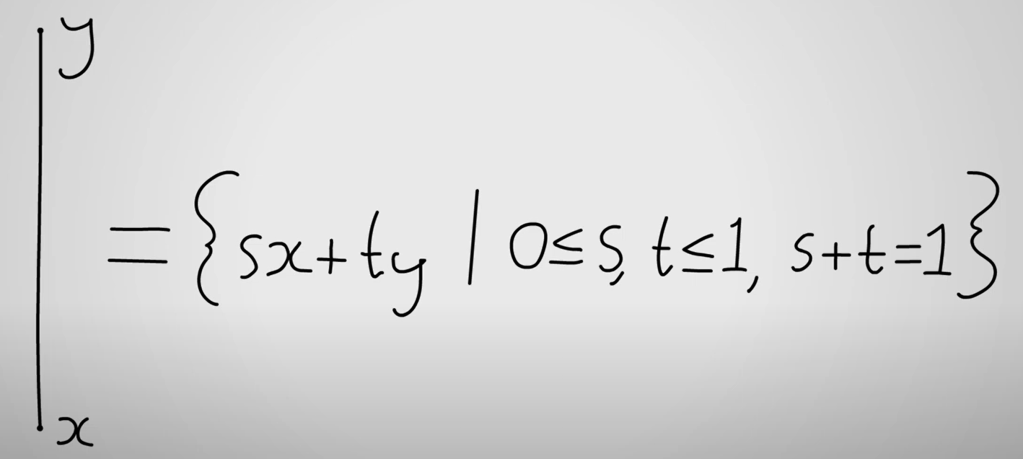
Follow the same line of reasoning, any dot in the triangle can be expressed

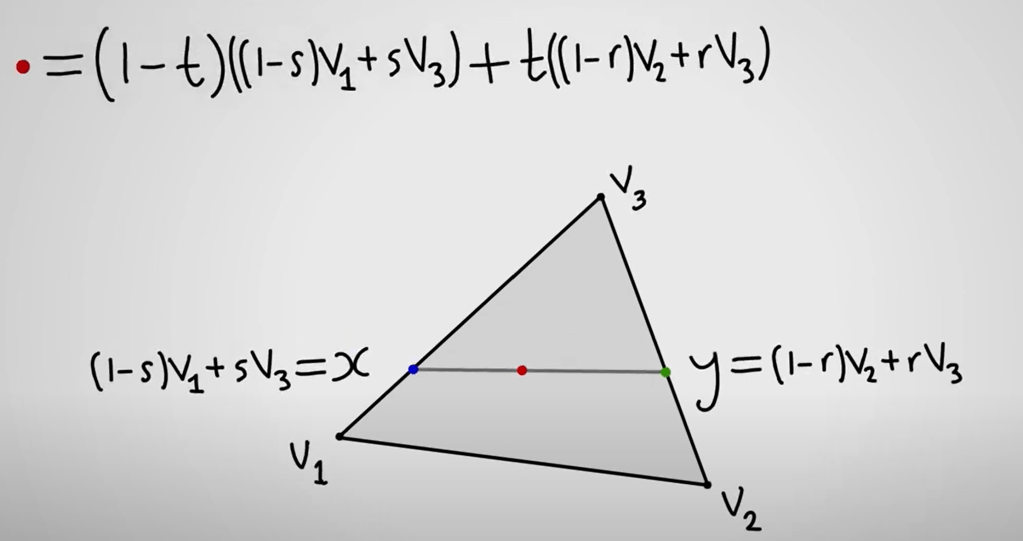
And summarize x = t1v1 + t2v2 + t3v3 satisfies t1+t2=t3 =1, 0 <= t1, t2, t3 <= 1

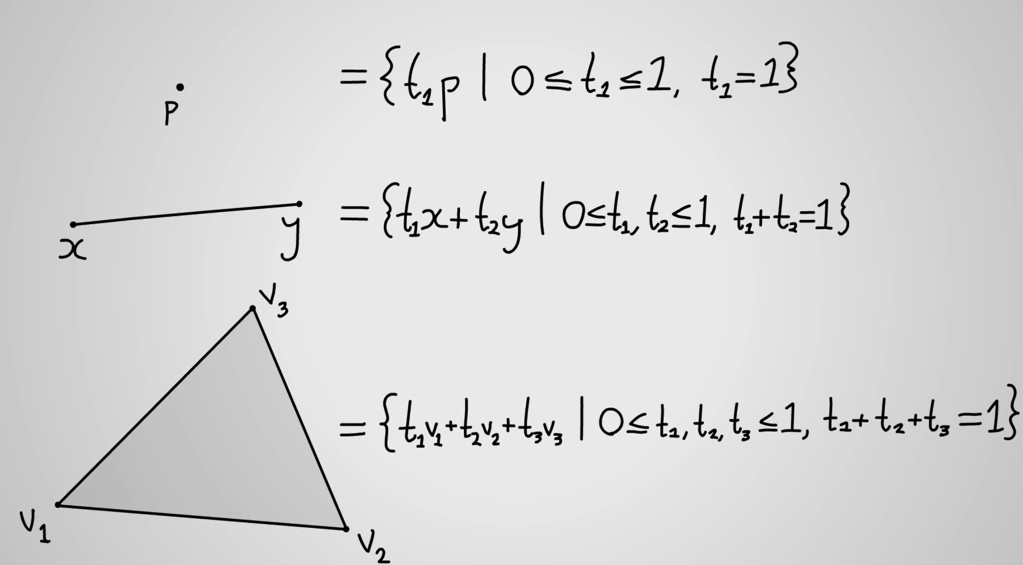
hence concept of n-simplex is introduced

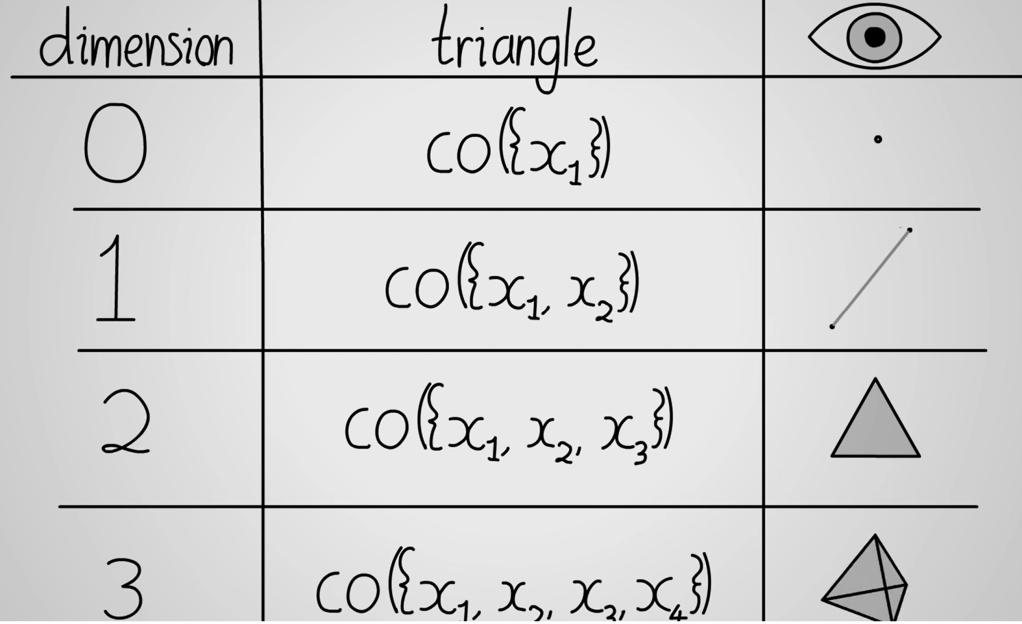
(note it’s referenced from boarbarktree)

Another fascinating example is Tensor. First I think of it as a matrix of various dimensions but then I realize not only matrix is inadequate to represent higher order/dimensions but also missed key element of denoting covariant or contravariant from symbolism perspective. Hence Tensor is a must to use tool for Einstein, he even invented Einstein summation symbol to save up time writing repetitive onerous sigmas.

For example in deducing the Dirac Equation for spinors, Professor Alex Fournoy didn’t show how Dirac’s ingenuity in figuring out matrix as square root of momentum 2-order equation, Alex instead start from SO(3) then to SO(1,3) with Lie Algebra, when describing a rotating angle in 3D versus 4D space, the complexity of the generator’s description makes it absolutely essential to use tensors: