The integral of a derivative in one dimension is a common concept, which is underscored by the Fundamental Theorem of Calculus. This theorem states that the definite integral of a function’s derivative over an interval from (a) to (b) with respect to (x) is equivalent to the difference in the function values at (b) and (a) (i.e., (f(b) – f(a))).

Extending this concept into higher dimensions, such as two or three dimensions, we encounter analogous principles in vector calculus, represented by curl and divergence respectively. Moving even further into higher dimensions, these ideas are generalized to address manifolds.

This foundational concept is central to Stokes’ Theorem in calculus, which articulates a relationship between the surface integrals and line integrals, extending the intuition from the Fundamental Theorem of Calculus to higher-dimensional spaces and complex geometric objects.

Using exterior algebra is highly effective for solving integral problems across multiple dimensions.

For instance, consider the task of computing the curl of a circular path within a vector field in (\mathbb{R}^2). Another example involves calculating the divergence of a spherical surface within a vector field in (\mathbb{R}^3). These scenarios illustrate the application of vector calculus in different dimensional contexts to analyze properties of vector fields related to circulation and flux.

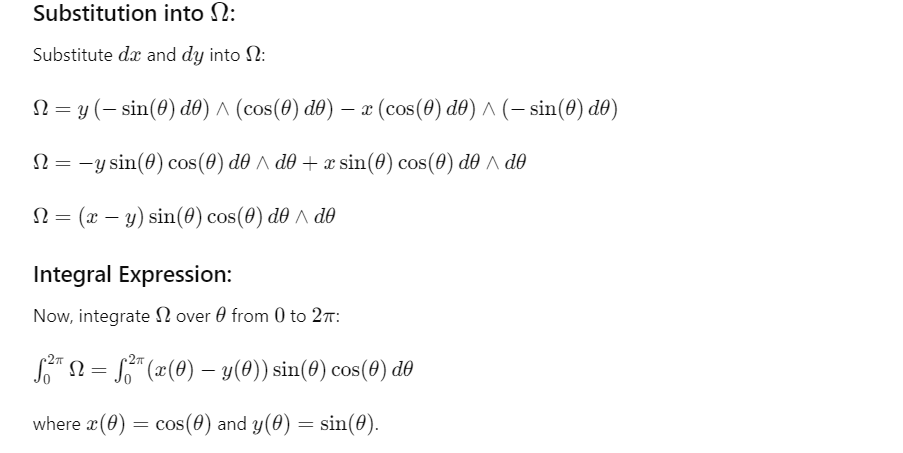
While the three dimensional example codes

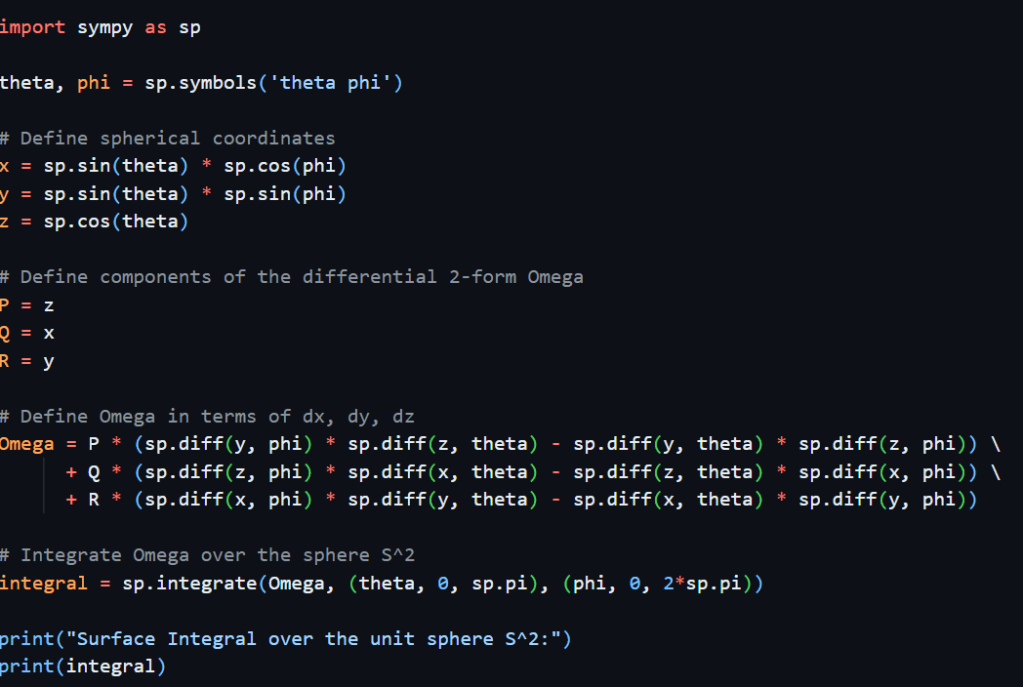
Even it’s only one line in codes, sp.itegrate(omega, (theta, 0, sp.pi), (phi, 0, 2*sp.pi)), the analytical process is as following:

Using traditional vector calculus is more cumbersome, reference below steps: