The mesh concept in discrete differential geometry is essentially consistent with the element in FEM:

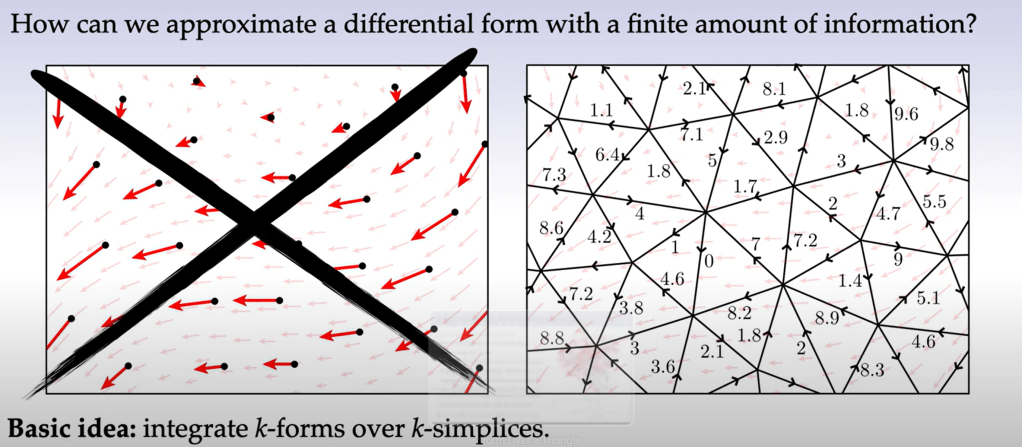
This mesh approach allows to do further rigorous computation to approximate any curvature, functions. Discretization just means integrate a k-form over k-simplices, result is just a list of values, so it’s easy to leverage matrix to compute.

Here is a good example to illustrate how applying this idea for a computation in 1-form:

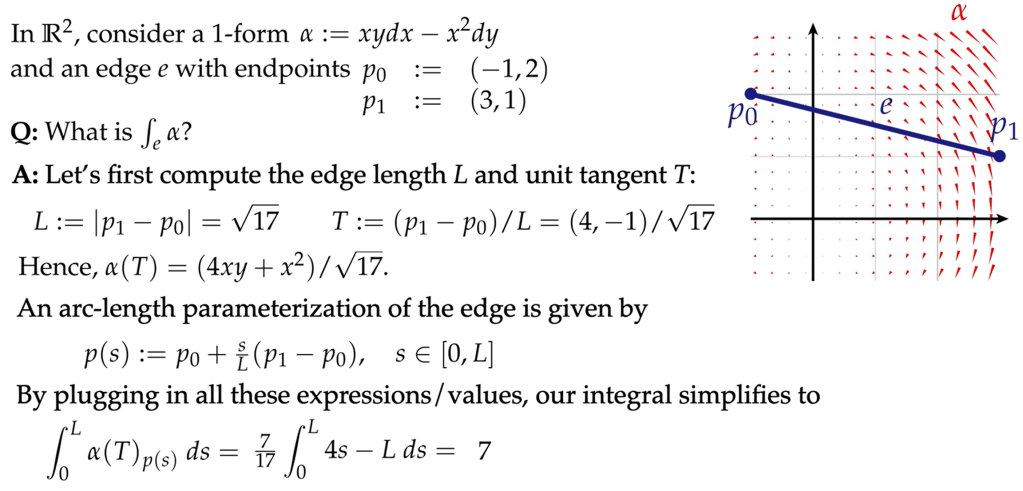
And on 2-form

Driving down to a discrete differential k-form, df, it is just any assignment of a value to each oriented k-simplex, why it’s an assignment of a value, due to the central theorem of calculus, or stoke’s theorem, df is just subtraction of boundaries. d can be thought of a map, “discretization” map, also integration of discretized derivatives.

It’s fundamentally related to advanced math concept of chain, co-chain and homology, cohomology:

The power of exterior calculus or algebra is manifested by the operators, in which, first of all, the boundary operator is essential:

it’s all from Keenan Crane.