Lagrange’s approach to algebraic curve, let’s say there is a function

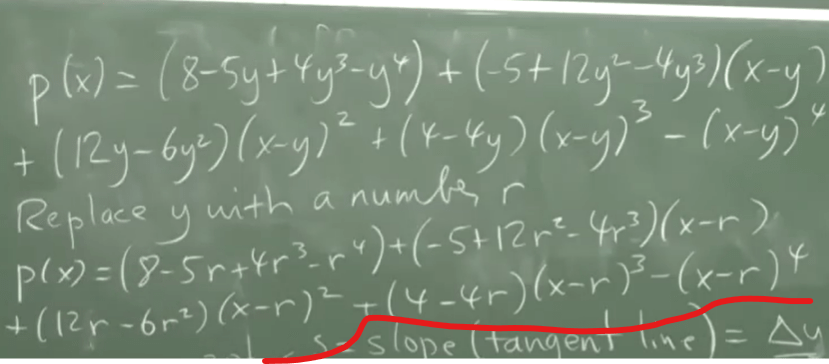
replacing y with r, a trick done to parameterize the curve, and his approach turns out magically same as Tayler’s expansion. It greatly helps mathematicians to understand the function value at r, or the zeroth approximation at r, then the tangent line to P at r, the tangent conic to P at r, and tangent cubic to P at r.

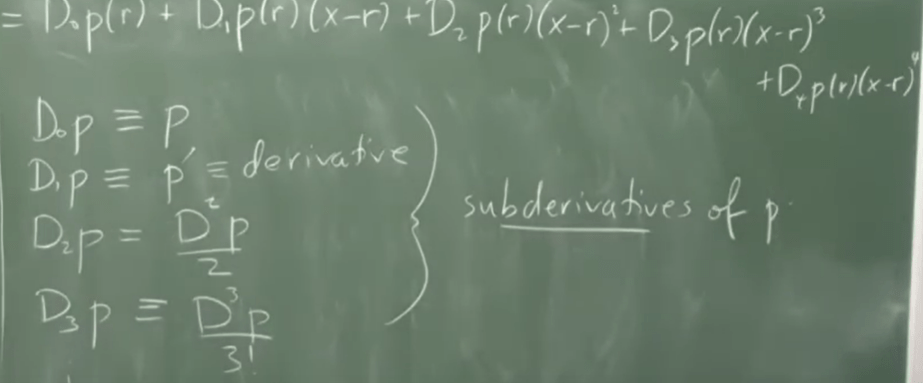
We got approximate function that is valid near point r. There is a theorem proved quite recently that for a cubic polynomial p(x), all the tangent conics Tr(2)P(x) are disjoint.

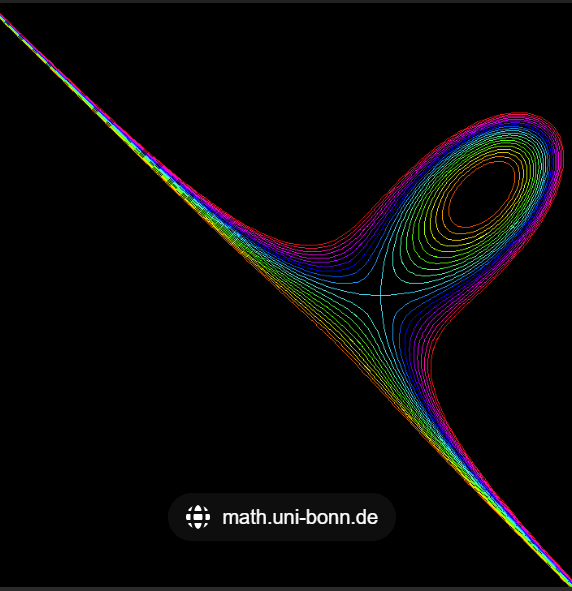
Then it’s natural to think about polynomials with two variables. so let’s look at folium P(x, y) = x^3 + y^3 + 3xy again, a good example of cubic surfaces, not cubic lines. We approach it with Lagrange’s again:

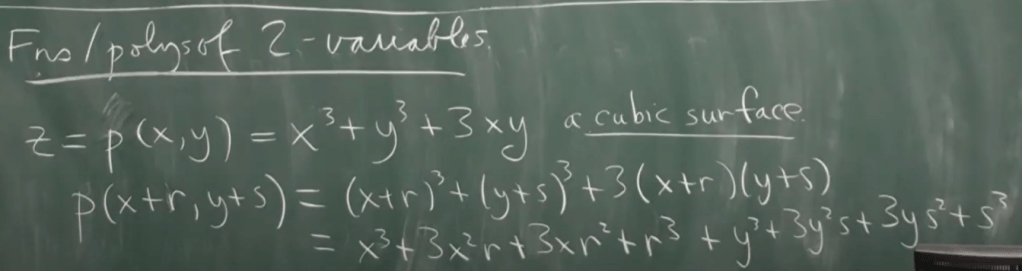
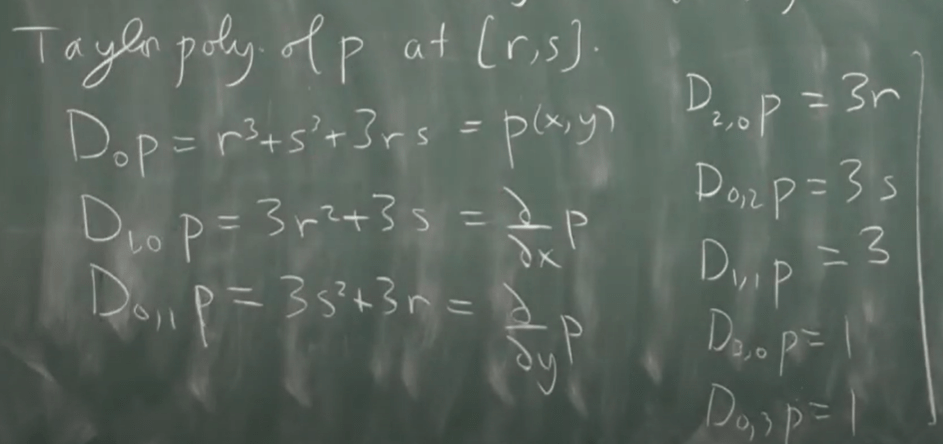
T(r, s)^(k)P = sum of all terms of total degree <= k (in x-r, y-s), when k=1, it’s the tangent plane approximating this cubic plane: r3 + s3 + 3rs + 3r^2 + 3s + 3s^2 + 3r. Moving on to tangent quadratic

Folium curves are a family of curves defined by a particular type of equation. The standard equation for a folium of Descartes is:

x3+y3−3axy=0

To plot this curve:

from NJ Wildberger

adding on terminology of conics and quadrics:

Conics are curves formed by intersecting a plane with a double-napped cone in two dimensions. Examples include circles, ellipses, parabolas, and hyperbolas.Quadrics are surfaces formed by second-degree polynomial equations in three dimensions. Examples include ellipsoids, hyperboloids, paraboloids, cones, and cylinders.