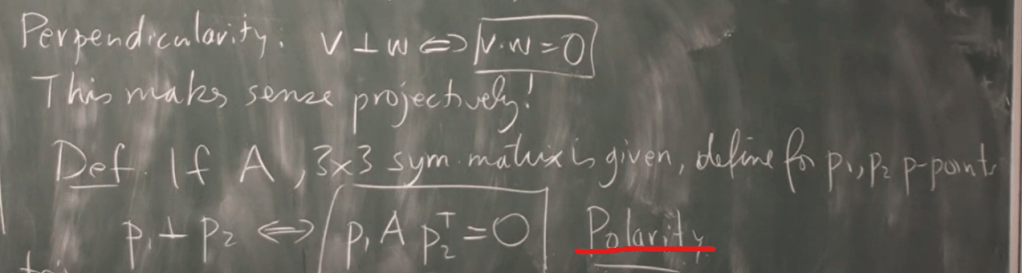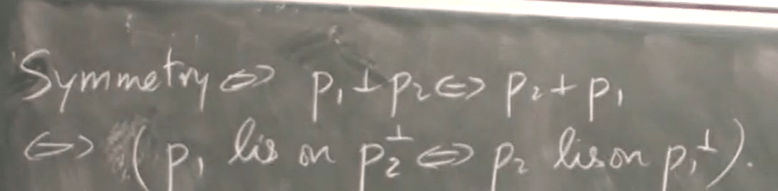Points and Lines form dual relationship, one is another’s duality. The line and points can be computed algebraically, for which basic understanding of cross product, determinant is needed:

Then introduce the concept of incidence as the point and line are incident, the row matrix P times the column matrix L = 0.

P lies on L or L passes through P. So we can see symmetry here and infer the Poppus theorem, points be collinear then lines are concurrent. To summarize these key concepts:

PL=0 incidence, joins (two points joins to form a line) and meets (two lines meets to locate a point), the algebraic forms are both cross product computation

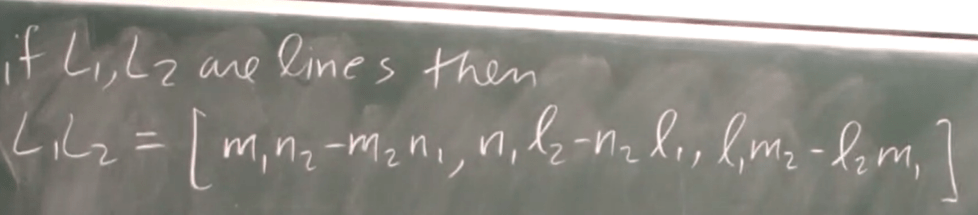
We say

There is great application of this projective geometry in transformation

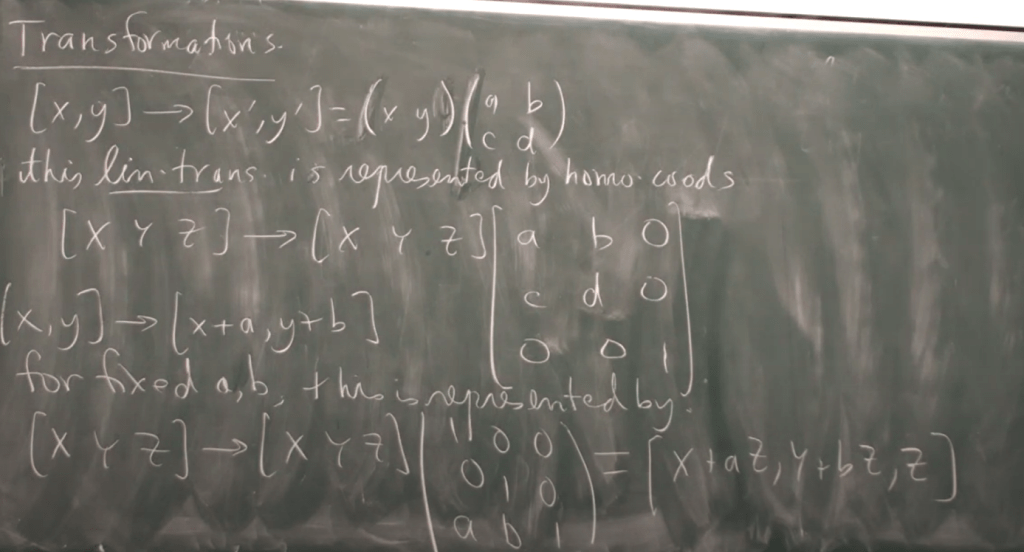
back to conic algebraic equation,

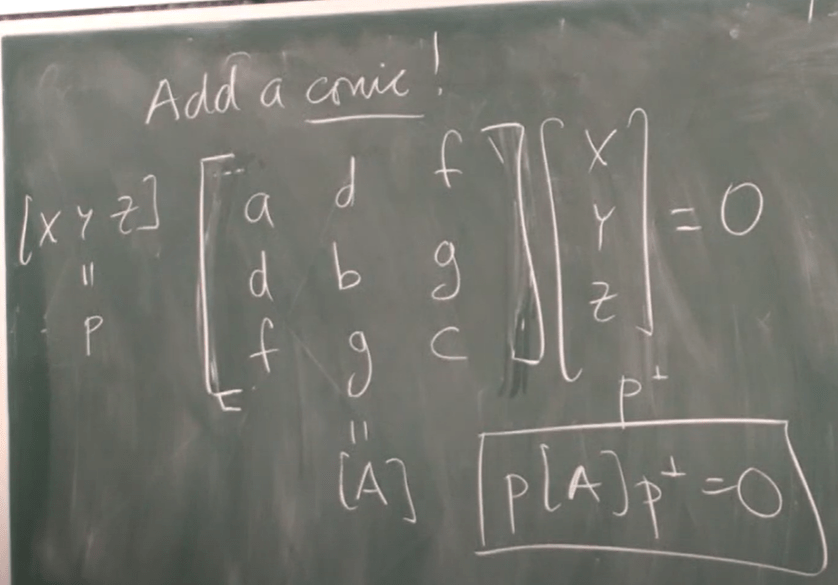
This matrix form is derived from

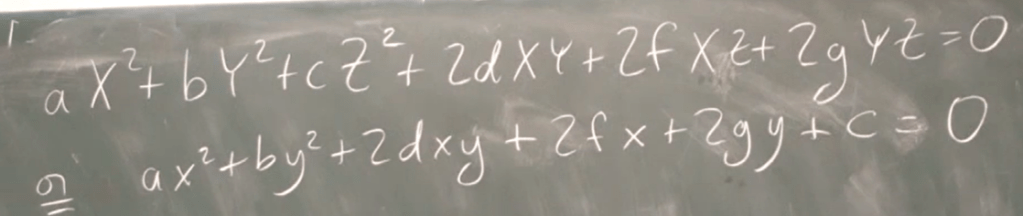
why it’s so important, because conic is essentially same as quadratic form, which is symmetric bilinear forms (or dot/inner product, v.w = vAw^T) , which is metrical structure. we can tell A is metric tensor, usually it’s a identity matrix, but also can be relativistic or Makowski matrix:

Further inference of v.w in projective plane, we can use it to define perpendicularity, then lead to the concept of polarity.