Applying TDA in time series, a simple approach is to break down segment of the curve into a bunch of data points, i.e. multi-dimensional data, this is parameterization, it forms point cloud:

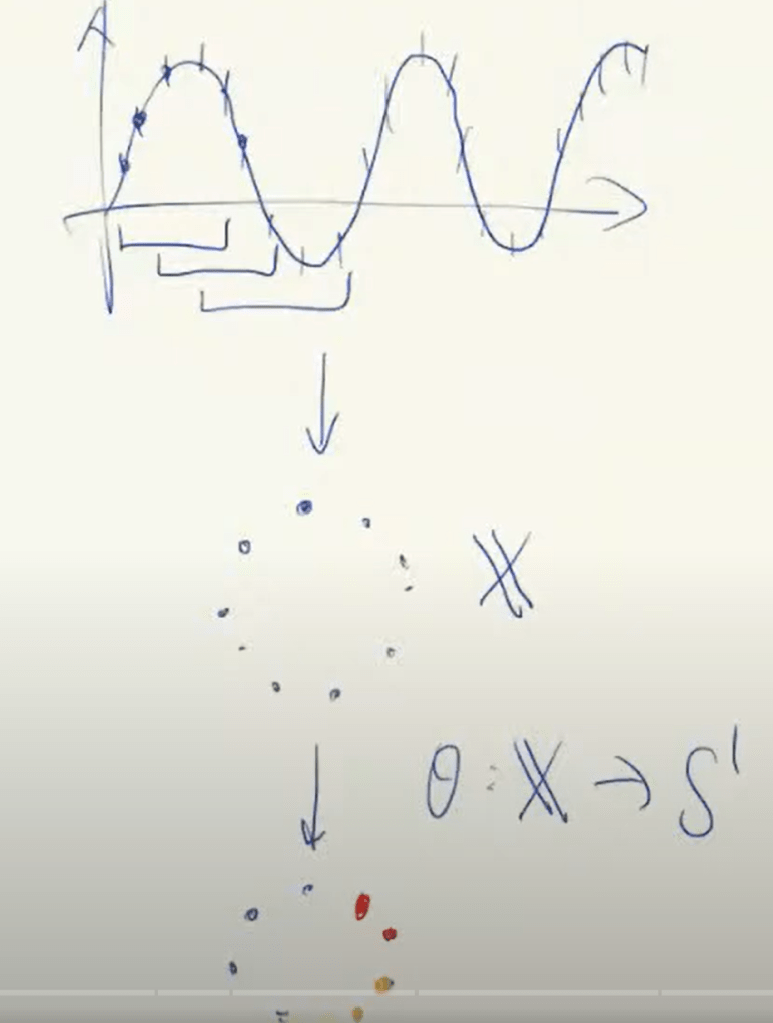
The essence of this approach is cohomology! Before jumping to cohomology, let’s ensure clear understanding of homology concepts: cycle, boundary and generator. its easier to intuitively, visually look at them: cycle bounds an empty loop/tunnel, boundary operator on cycle = 0; while boundary bounds filled space, generator is somewhat the holes, betti number, that’s the basis element to generate the entire group. so like torus’s generator is the two loop one around the circle, the other horizontal cut.

In cohomology, it’s dual relationship, so there is cocycle, coboundary.

First introduce the concept of element cochain, corresponding to chain element, symbolize chain to bottom right corner, symbolize cochain in upper right corner, element of chain without asterisk, while cochain element denoted with asterisk on the upper right corner.

element zero cochain(vertex), element 1 cochain(edge), element 2 cochain(triangle) is a function that operators on the element chain and spit out a scaler. The gist is here: chain and cochain(function) makes computation of simplex algebraic!

The coboundary operation is mind-twisting:

to look at the adjacencies one dimension higher (boundary is lower)

from Dr. Bei Wang