There are two ways to describe an mathematical object, explicit and implicit. For example, a circle can be described as x square + y square – 1 = 0 implicitly or as to construct the components explicitly as x = cos(theta) and y = sin(theta).

So in linear algebra, the kernel of phi to represent objects in vector space V is implicit, while on the other direction, direction flowing from upstream, the image of sai is explicitly describing objects in V. And image of sai is contained in kernal of phai, but if everything is exact, then they are equal or “exact”.

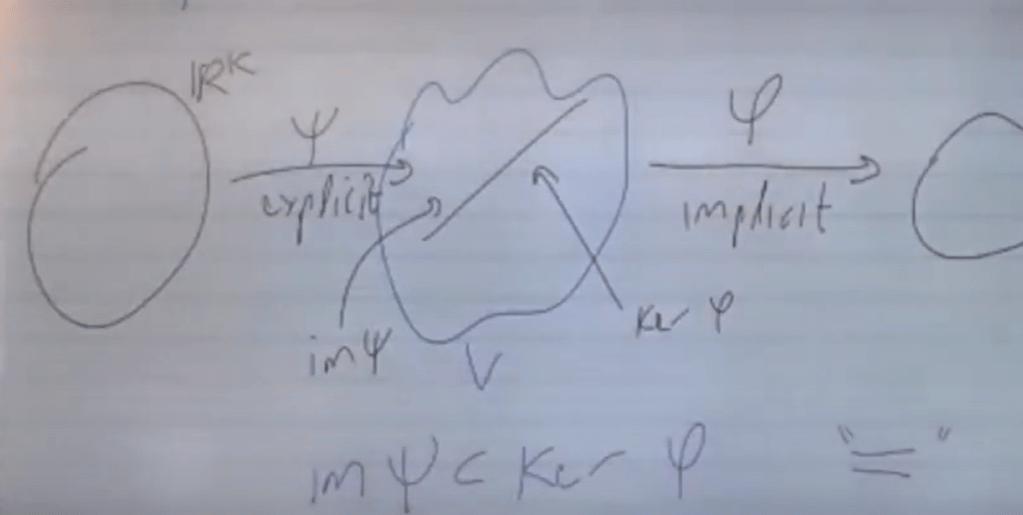
it’s homology. the difference or modula between the kenel of phi and image of sai is the Hn. the number of holes, or in other perspective, homology describe how good do you construct things, did it describe “exactly” or leave something out.

and cohomology is same just reversing the sequence.

What an insight! Master’s able to identify the essence without teaching you mechanical rules and formulas.

Now let’s use this perspective to connect homology and De Rham cohomology.