When studying topology, knowing real number space R, can help to understand R2 = RxR, R3…, it looks like cartesian product and is deeply related to internal direct products in Group theory.

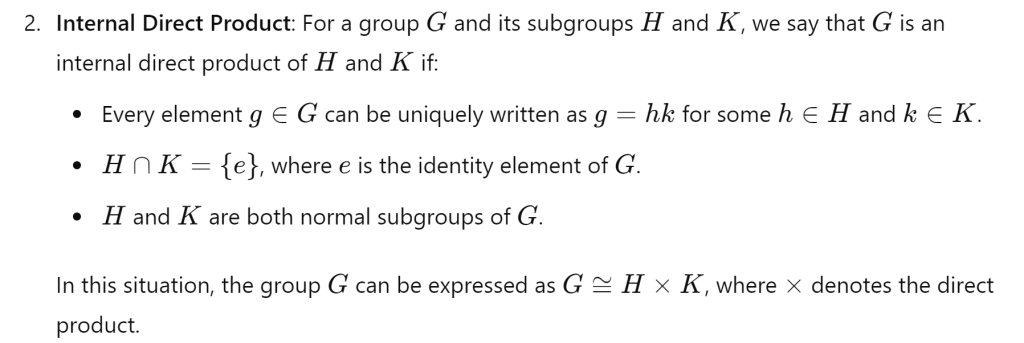
Note to differentiate it from Direct Product

while the direct product of groups combines them in a structured way, the internal direct product allows you to decompose a group into simpler, well-understood subgroups within itself.

Another example using S3 and A3:

What is external direct product

Here is something to be proved: relative primes implies cyclic:

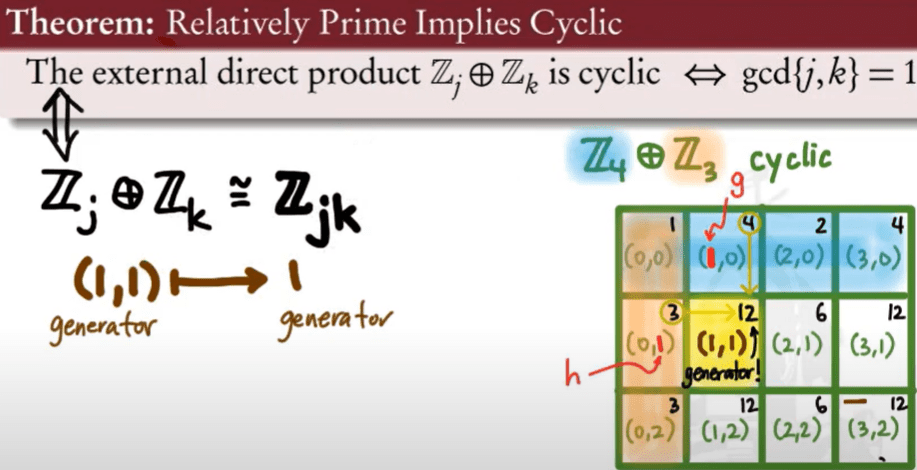
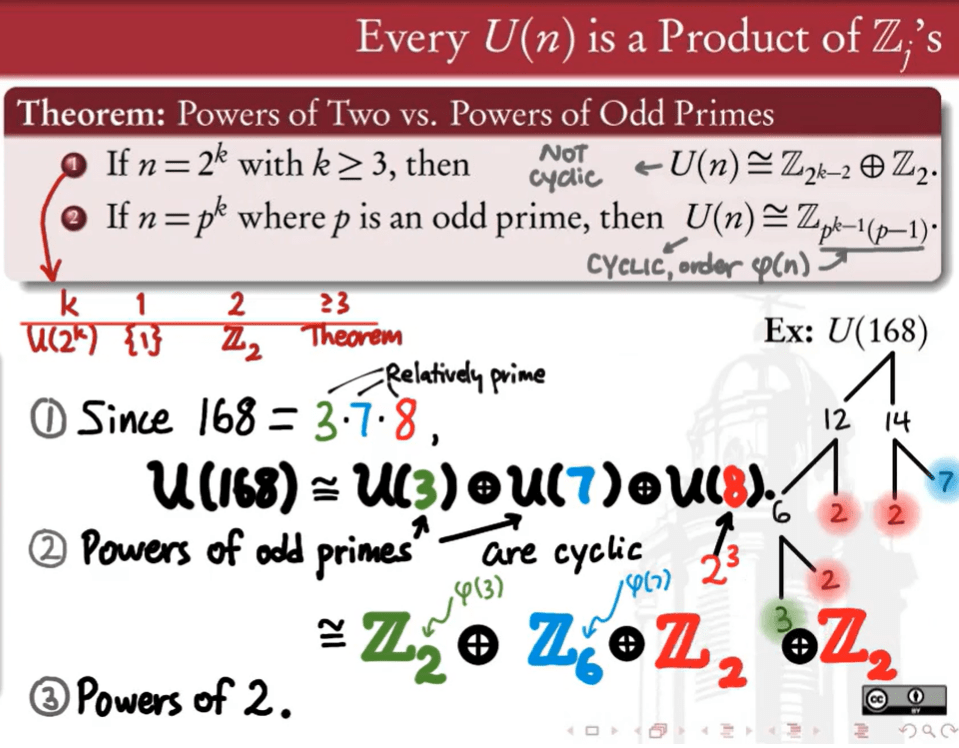
This has profound application to deconstruct a multiplicative group say U(168), 168 is the product of relative primed factorization 3, 7, 8, then U(168) is isomorphic to the direct product of U(3), U(7) and U(8).

introduce the concept of short exact sequence

and here is the key: the image of function g is identical to the kernel of function f! And that’s what gets to be called EXACT sequence.

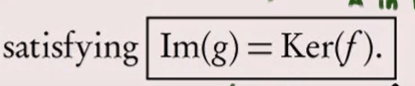
Why this short exact sequence is so important, it could help us construct or decompose groups:

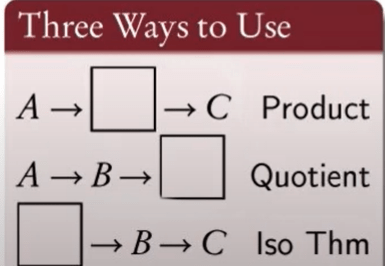
So the first scenario A and C can deduce B via product, there are multiple ways actually, what’s straight forward is direct product, and there is semi-direct product.

This helps/leads to more fundamental concepts such as normal subgroup, quotient or factor group.

Need to know the difference between internal and external direct product