It’s interesting to review control theory in dynamic systems, such as classical control techniques and the ordinary differential equation (ODE) systems and apply in ROS to make robot system stable like how we study spring and pendulum and learn how to stabilize them.

Revisit Steve Brunton’s control bootcamp series to fresh up classical ODE

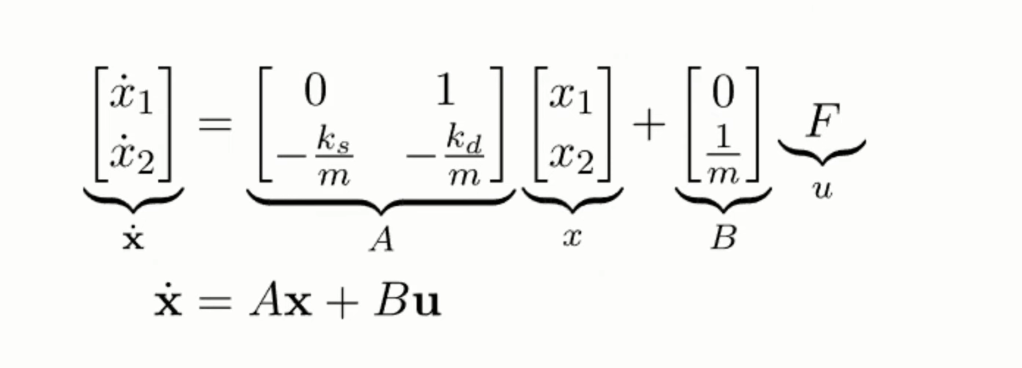
x̄ = Ax, x̄ ∈ ℝⁿ

x(t) = e^(At) x(0)

e^(At) = I + At + (A²t²)/2! + (A³t³)/3! + …

Eigenvalues & Eigenvectors:

AT = TDT⁻¹AT = D5. [T,D] = eig(A)

It’s essential to understand using eigen conversion so the system is much easier to solve as it’s converted to a orthogonal system.

further inference, we find the stability is decided by the lambda, the left side would be stable.

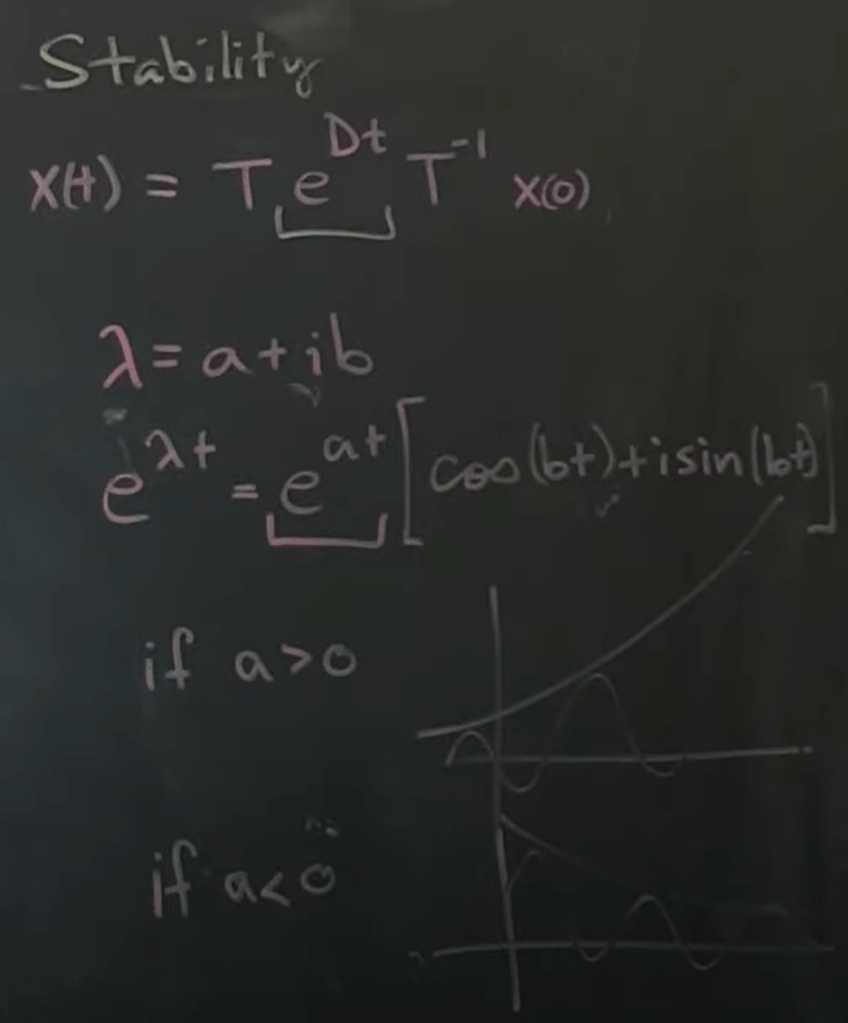
Linearizing Around a Fixed Point:

first use this simple pendulum example to write down the Jacobian equation:

ẋ₁ = f₁(x₁, x₂) = x₁x₂

ẋ₂ = f₂(x₁, x₂) = x₁² + x₂²

Df/Dx = [∂f₁/∂x₁ ∂f₁/∂x₂][∂f₂/∂x₁ ∂f₂/∂x₂]= [x₂ x₁][2x₁ 2x₂]

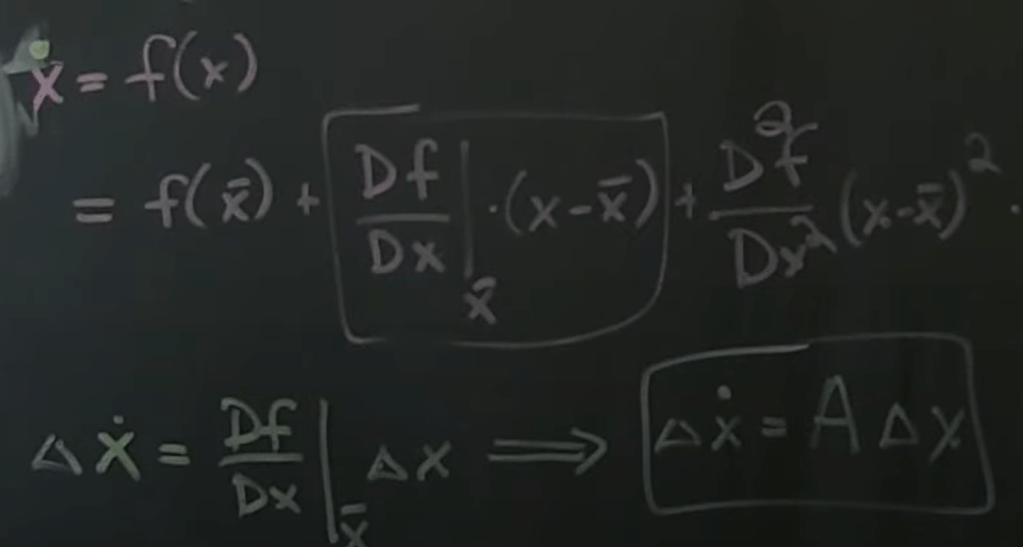
above equation we can see the first order differentiation on the vector function f is Jacobian matrix, which is consistent to the concept of tangent space/lie algebra on lie group. such computations are common in robotics and particularly in ROS (Robot Operating System). In robotics, Lie groups and algebras are often used for representing and manipulating 3D transformations, which is crucial for tasks like robot kinematics, motion planning, and state estimation.Here are some examples in both C++ and Python that demonstrate how these concepts are applied in robotics contexts:

here is sample C++ codes using the Eigen and sophus library

#include <iostream>
#include <Eigen/Core>
#include <Eigen/Geometry>
#include <sophus/se3.hpp>

int main() {
    // Create a 3D rotation (SO(3) element)
    Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/4, Eigen::Vector3d::UnitZ()).toRotationMatrix();
    
    // Create a translation
    Eigen::Vector3d t(1, 2, 3);
    
    // Create an SE(3) transformation
    Sophus::SE3d T(R, t);
    
    // Get the Lie algebra (se(3)) representation
    Eigen::Matrix<double, 6, 1> se3 = T.log();
    
    std::cout << "SE(3) as Lie algebra:\n" << se3 << std::endl;
    
    // Compute the Jacobian (in this case, the left Jacobian of SE(3))
    Eigen::Matrix<double, 6, 6> J = Sophus::leftJacobianSE3(se3);
    
    std::cout << "Left Jacobian of SE(3):\n" << J << std::endl;
    
    return 0;
}

The Linear Quadratic Regulator (LQR) is an optimal control algorithm that solves the problem of finding the best control law for a given dynamic system to minimize a cost function. It is widely used in control theory, robotics.