Diving deeper into Makemore codes to illustrate subtle details affecting the nn output. For example, the concept of “dead neurons” if the squashing function, say, tanh squashed too many inputs to the polar data points of -1 and +1, causing previous neuron’s gradients killed:

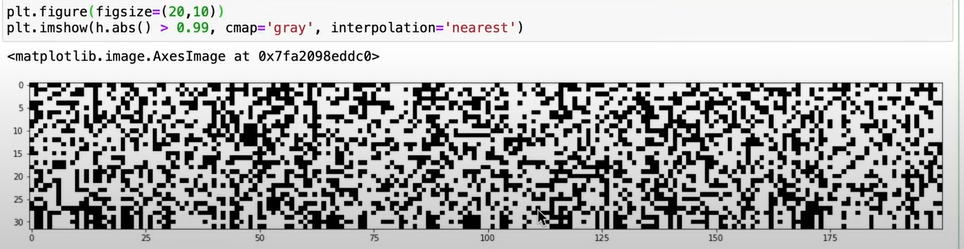
By resetting the scale of the weights and bias initialized, the problem can be dealt with.

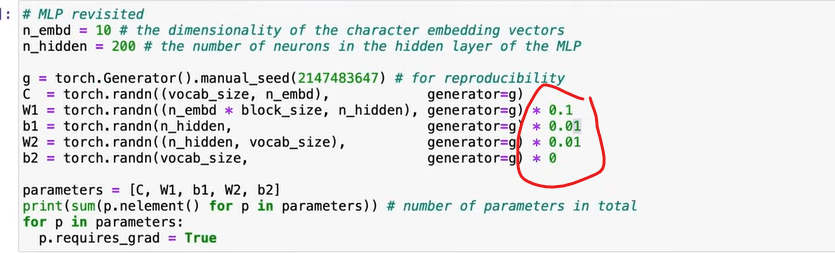
Next, how to set up or scale these weight/bias initialization, in setting randn for x and w as below codes, problem generated as the y’s standard deviation is 3 times more. See the plots below, our human eyes would think the right one is narrower/more lean, but it’s opposite:

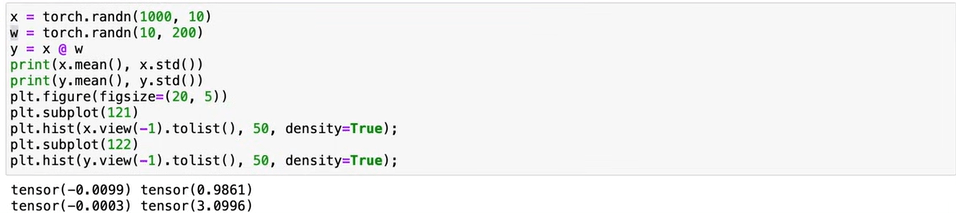
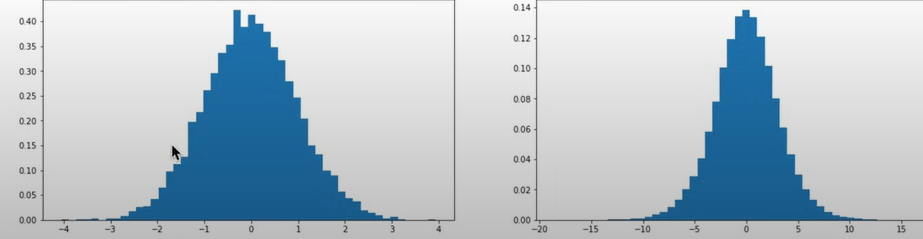
The left histogram is narrower, meaning the data points are closer to the mean. This suggests a lower standard deviation.The right histogram is wider, indicating that the data points are more spread out. This suggests a higher standard deviation. (per chatGPT)

BatchNorm solve this problem of tweaking initials, but there is a caveat, it needs to be scaled and shifted on top of normalization.

BatchNorm introduced is an effective way it stabilize training to with side effect of regularization. But it does introduce potential jittering bugs as it arbitrarily padded in an entirely random set of data.

class Linear:
  def __init__(self, fan_in, fan_out, bias=True):
    self.weight = torch.randn(fan_in, fan_out), generator=g) / fan_in**0.5
    self.bias = torch.zeros(fan_out) if bias else None
  def __call__(self, x):
    self.out = x @ self.weight
    if self.bias is not None:
      self.out += self.bias
      return self.ouat
  def parameters(self):
    return [self.weight] + ([] if self.bias is None else [self.bias])

In manually deduce/compute backprop, the first one is to deeply understand why the dlogprobs manually computed in top area is identical to the dnorm_logits:

# Calculate the gradient of logprobs manually
dlogprobs = torch.zeros_like(logprobs)
dlogprobs[range(n), Yb] = -1.0 / n

# Backpropagate through the probability calculations
dprobs = (1.0 / probs) * dlogprobs
dcounts = counts_sum_inv * dprobs
dcounts_sum_inv = (counts * dprobs).sum(1, keepdims=True)
dcounts_sum = (-counts_sum**-2) * dcounts_sum_inv
dcounts += torch.ones_like(counts) * dcounts_sum
dnorm_logits = counts * dcounts

here N is 32 (batch size), then the gradient value is -1/32. Depending on actual Yb index value from 0 to 31, the position of -1/N show up in that matrix or tensor:

tensor([ 8, 14, 15, 22,  0, 19,  9, 14,  5,  1, 20,  3,  8, 14, 12,  0, 11,  0,
        26,  9, 25,  0,  1,  1,  7, 18,  9,  3,  5,  9,  0, 18]) Yb
tensor([[ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,
         -0.0312,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,
          0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,
          0.0000,  0.0000,  0.0000],
        [ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,
          0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000, -0.0312,  0.0000,
          0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,
          0.0000,  0.0000,  0.0000],