Revisiting the concept of tensor in April 2025 per inspiration from “abide by reason”. The key is to grasp concept of dual space, (where df in differential geometry live too). It’s essentially a “linear functional” that takes in element in vector space and spit out real number in R.

Tensor’s concept is the expansion on that linear functional, it’s on various dimensions on both dual space and vector space. TENSOR is a map. some examples

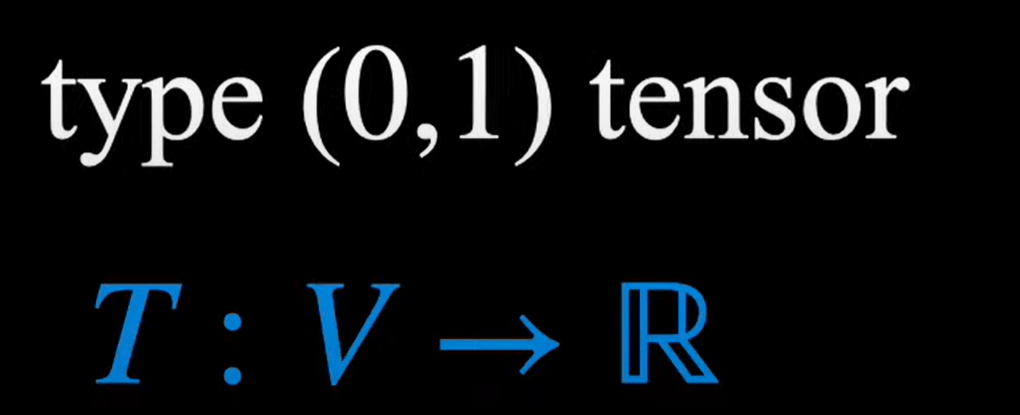
this tensor takes in a vector generates a real number, it’s exactly the dual vector

This is a vector, it takes in a dual vector and generates a real number.

What is Tensor? Tensor is an invariant geometric object. But that’s too abstract, let’s start from understanding two familiar tensors – metric tensor and stress tensor!

The metric tensor itself is an invariant, geometric object—it represents the fundamental structure of space(time), independent of the coordinate system.

However, its components gμνg_{\mu\nu}gμν​ are not invariant; they change when switching coordinate systems.

The stress tensor is also a geometric object, just like the metric tensor. But instead of defining distances and angles, it describes the distribution of forces and momentum flux in a material or spacetime.

Let’s break it down intuitively.

The stress tensor transforms like any other tensor under coordinate transformations.