The determinant is a single number associated with a square matrix that tells you how the matrix transforms space. Intuitively, you can think of it as a scaling factor for volume and a test for invertibility.

1. Volume Interpretation:
   • Imagine a 2×2 matrix as a transformation applied to a unit square. The determinant tells you how the area of the transformed shape changes:
     • det⁡>0\det > 0det>0 → The area is preserved (possibly stretched or shrunk, but orientation is the same).
     • det⁡<0\det < 0det<0 → The area is preserved but flipped (like a reflection).
     • det⁡=0\det = 0det=0 → The area collapses to a line (losing a dimension).
   • In 3D, the determinant tells you how a cube’s volume is changed.
2. Invertibility:
   • If det⁡A=0\det A = 0detA=0, the transformation squashes space in a way that information is lost, making it non-invertible.
   • If det⁡A≠0\det A \neq 0detA=0, the transformation preserves some structure and is invertible.
3. Direction and Orientation:
   • A positive determinant means the transformation preserves the original “handedness” of space.
   • A negative determinant means the transformation flips it, like switching from a right-handed to a left-handed coordinate system.

Exterior algebra is a mathematical structure that extends linear algebra to handle oriented areas, volumes, and higher-dimensional objects using a formal system of “wedge products.” It is fundamental in differential geometry, gauge theory, and physics.

Why Is Exterior Algebra Important?

1. Generalizes Determinants and Cross Products
   • The determinant can be understood through wedge products.
   • The cross product in 3D is a special case of the wedge product in Λ2V\Lambda^2 VΛ2V.
2. Useful in Gauge Theory and Physics
   • Gauge fields (like the electromagnetic field tensor) are expressed as differential forms.
   • The exterior derivative and wedge product elegantly describe field strength tensors.
3. Describes Volume and Orientation
   • In higher dimensions, it allows a natural way to compute areas, volumes, and their generalizations.

In Exterior Algebra, see how determinant is generated:

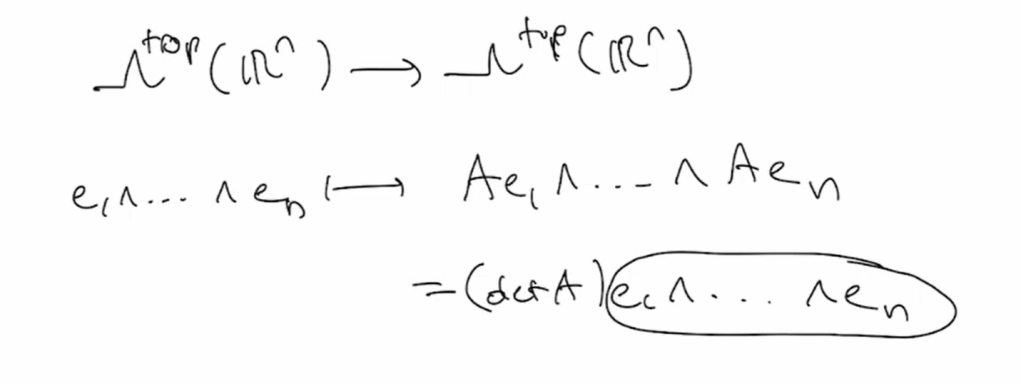
According to the original understanding of determinant as the “increased/decreased” area after the matrix transformation, it does make a lot of sense it’s function in this exterior algebra.