what’s the definition of differential forms?

k-forms are those that can integrate on k-dimensional domains or manifolds. Given what discussed about pull back of function and push forward, it’s the same concept just expanded to higher dimensions:

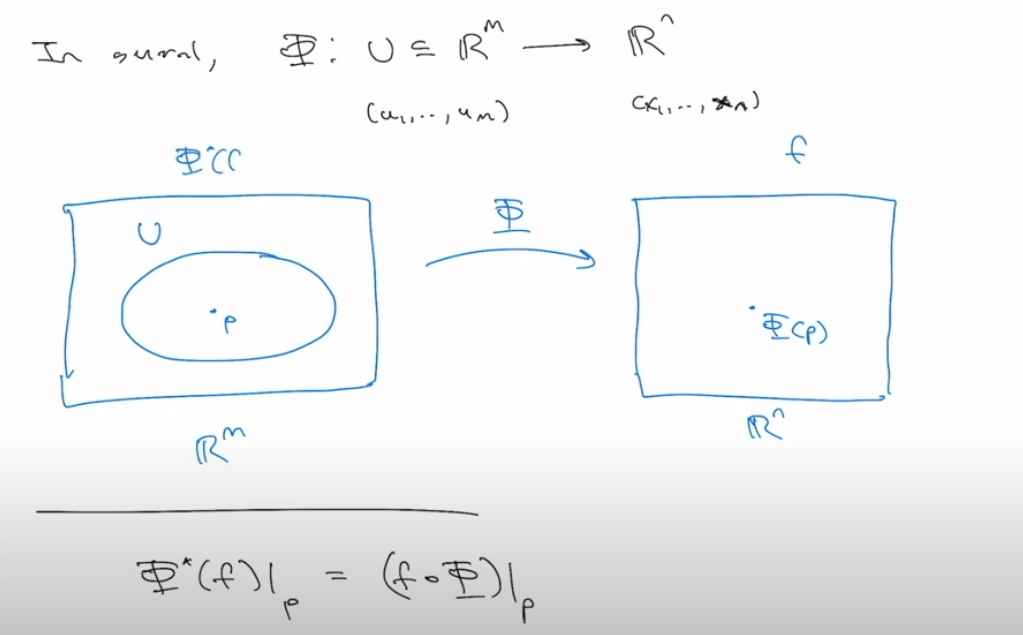
the purpose is to pull back differential forms by passing through wedges:

Contraction operator? it’s written as below and understood as we feed the tangent vectors to cotangent vector

so for any general tangent vector, that is contracted to dx j, we dot this v j in Einstein Notation.

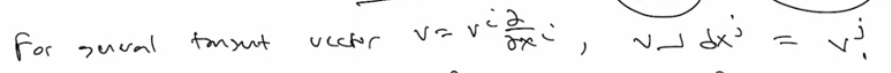
contraction lowers degree of k-forms

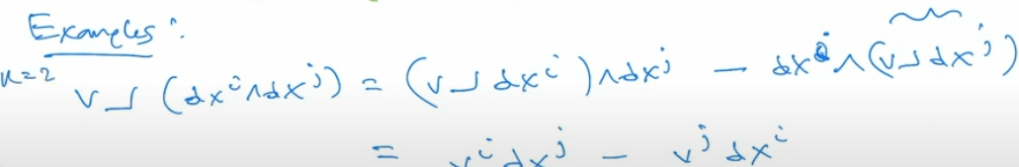
now integration! integrate omega along gamma:

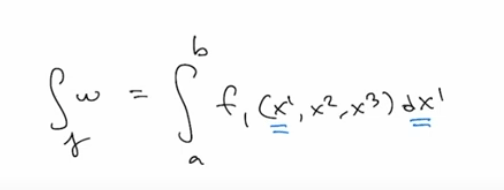
example n=2, integration of 1-form to enhance the understanding!

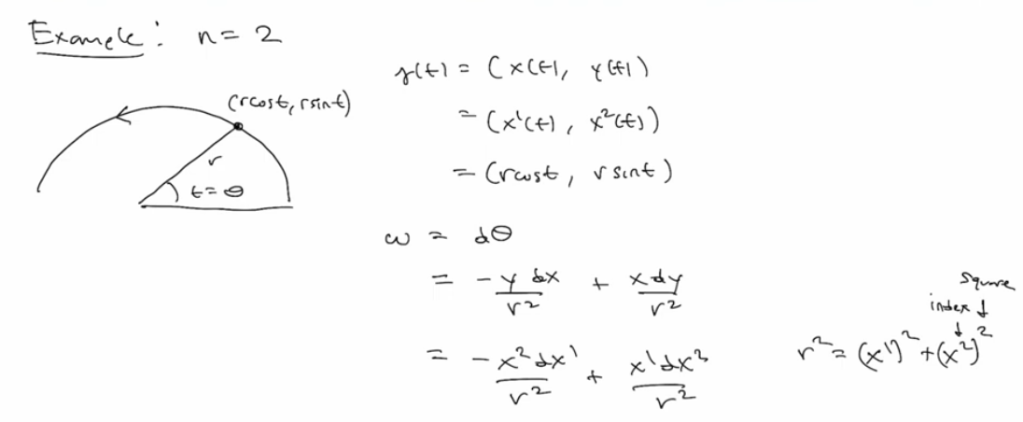
Now to integrate 2-forms surface to enhance understanding:

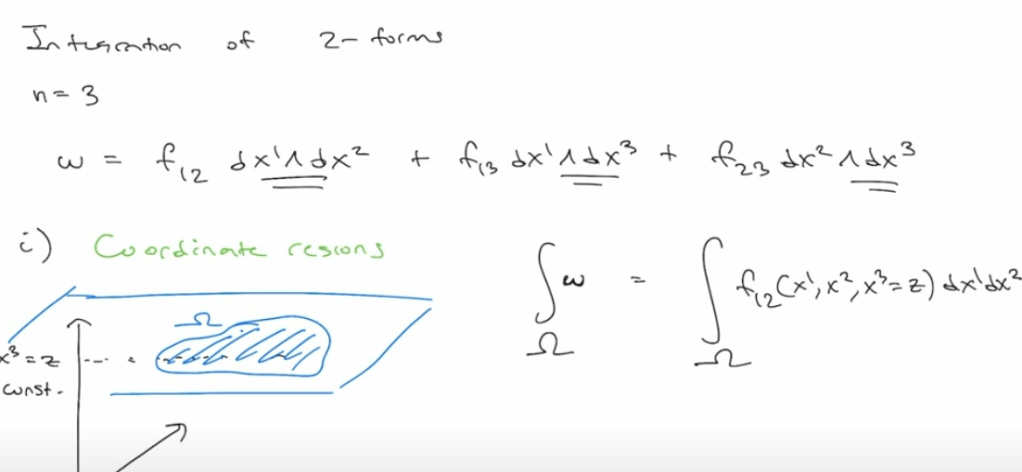
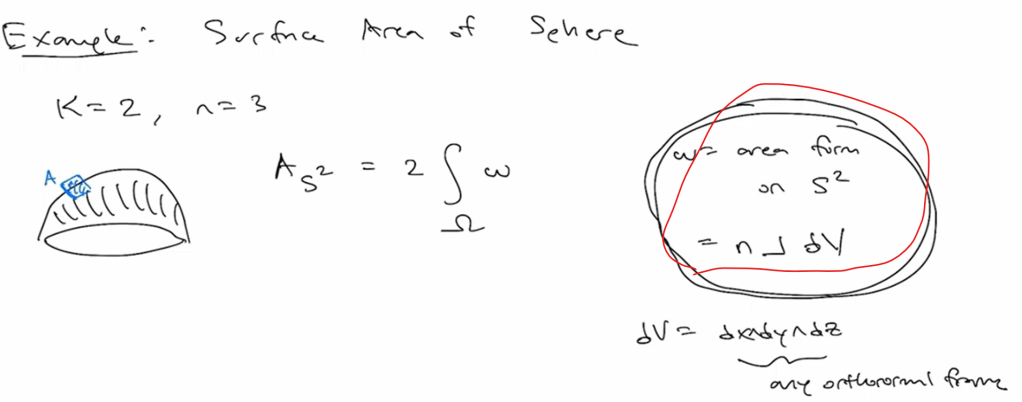
taking to a higher level of complexity by calculating generic surface area such as

Another example is to compute the area of a sphere, the key here is to understand the w = n contract dV.