In calculus, we learn that the derivative measures change. But in a deeper mathematical sense, differentiation acts as the opposite of taking a boundary. This idea is best understood using the language of differential forms and chains.

At its core, differentiation isn’t just about slopes—it’s about how things flow across a space. And just as boundaries “trap” something inside, derivatives measure how things “escape” or spread out. Let’s explore this intuition using chains (homology) and forms (cohomology).

Now, let’s connect these ideas.

• Boundaries “enclose” things—they define limits and prevent things from escaping.
• Derivatives describe “flows” and how things escape from a region.

This is why the exterior derivative ddd (which acts on forms) is the dual of the boundary operator ∂\partial∂ (which acts on chains).

In a sense, taking a boundary restricts motion, while taking a derivative measures motion.

Adding this insight for future elaboration:

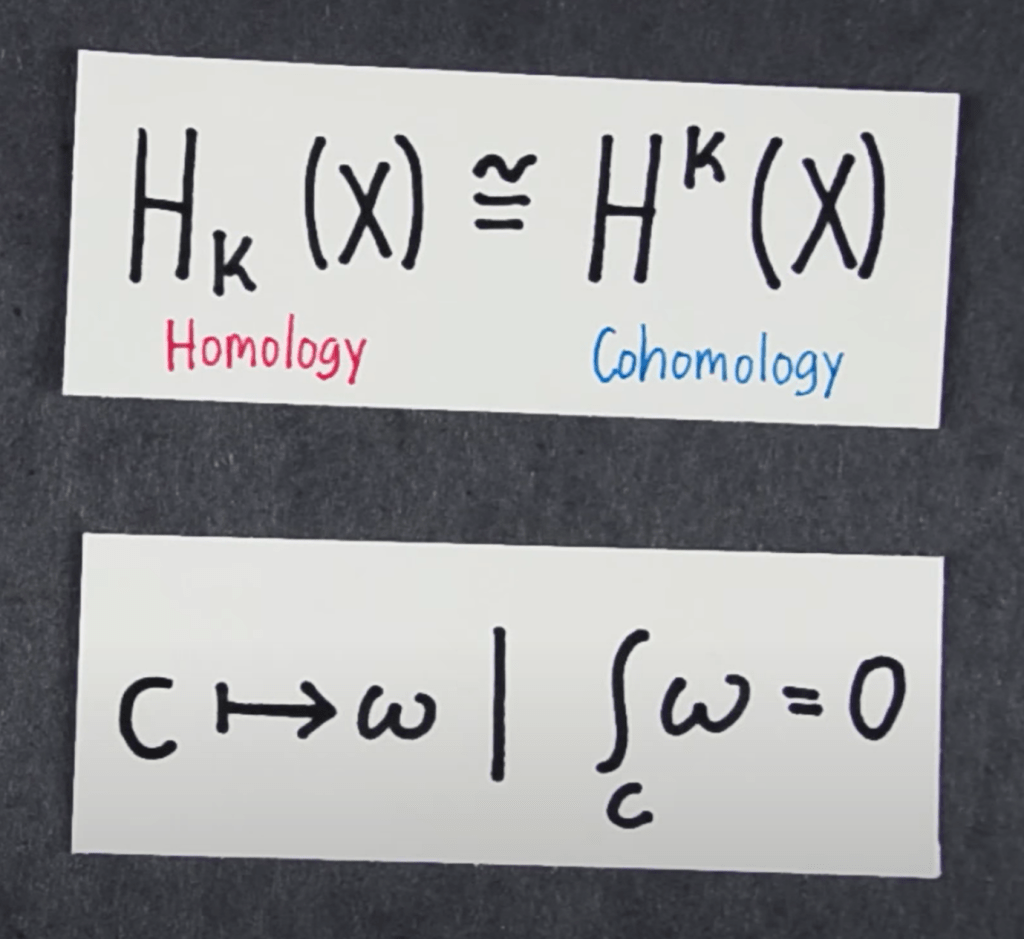
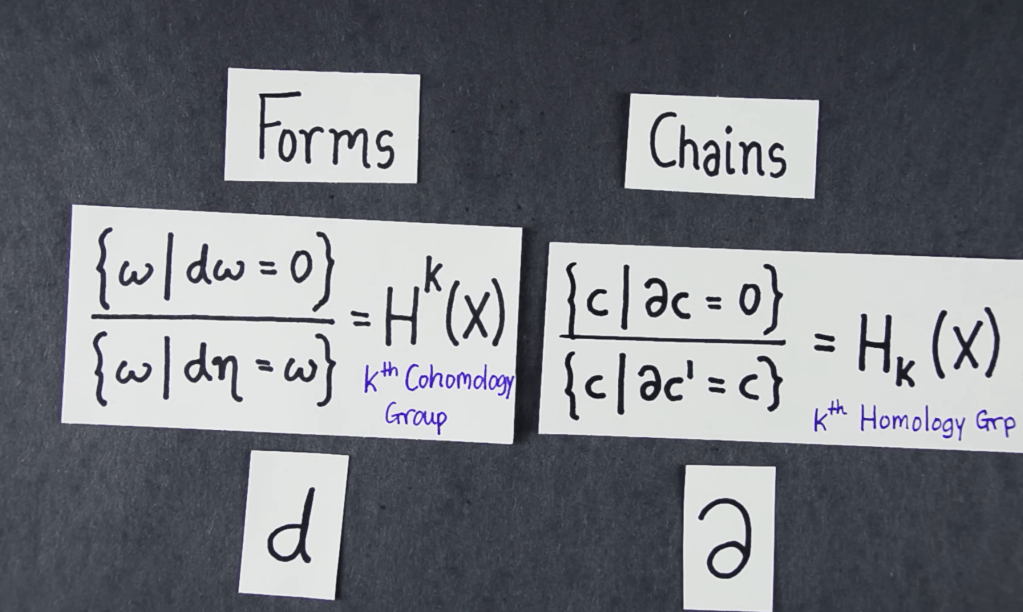
Chains describe shape while forms describe flow, motion, changes!