If you truly understand a theory, you can code it up and run it. So is my approach to truly understanding q, k and v in transformer’s attention mechanism.

in Previous blog, using “the cat chased the mouse” as an example the math is illustrated in details. Now apply it in codes (from Andrej Kaparthy):

class CausalSelfAttention(nn.Module):

    def __init__(self, config):
        super().__init__()
        assert config.n_embd % config.n_head == 0
        # key, query, value projections for all heads, but in a batch
        self.c_attn = nn.Linear(config.n_embd, 3 * config.n_embd, bias=config.bias)
        # output projection
        self.c_proj = nn.Linear(config.n_embd, config.n_embd, bias=config.bias)
        # regularization
        self.attn_dropout = nn.Dropout(config.dropout)
        self.resid_dropout = nn.Dropout(config.dropout)
        self.n_head = config.n_head
        self.n_embd = config.n_embd
        self.dropout = config.dropout
        # flash attention make GPU go brrrrr but support is only in PyTorch >= 2.0
        self.flash = hasattr(torch.nn.functional, 'scaled_dot_product_attention')
        if not self.flash:
            print("WARNING: using slow attention. Flash Attention requires PyTorch >= 2.0")
            # causal mask to ensure that attention is only applied to the left in the input sequence
            self.register_buffer("bias", torch.tril(torch.ones(config.block_size, config.block_size))
                                        .view(1, 1, config.block_size, config.block_size))

    def forward(self, x):
        B, T, C = x.size() # batch size, sequence length, embedding dimensionality (n_embd)

        # calculate query, key, values for all heads in batch and move head forward to be the batch dim
        q, k, v  = self.c_attn(x).split(self.n_embd, dim=2)
        k = k.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        q = q.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)
        v = v.view(B, T, self.n_head, C // self.n_head).transpose(1, 2) # (B, nh, T, hs)

        # causal self-attention; Self-attend: (B, nh, T, hs) x (B, nh, hs, T) -> (B, nh, T, T)
        if self.flash:
            # efficient attention using Flash Attention CUDA kernels
            y = torch.nn.functional.scaled_dot_product_attention(q, k, v, attn_mask=None, dropout_p=self.dropout if self.training else 0, is_causal=True)
        else:
            # manual implementation of attention
            att = (q @ k.transpose(-2, -1)) * (1.0 / math.sqrt(k.size(-1)))
            att = att.masked_fill(self.bias[:,:,:T,:T] == 0, float('-inf'))
            att = F.softmax(att, dim=-1)
            att = self.attn_dropout(att)
            y = att @ v # (B, nh, T, T) x (B, nh, T, hs) -> (B, nh, T, hs)
        y = y.transpose(1, 2).contiguous().view(B, T, C) # re-assemble all head outputs side by side

        # output projection
        y = self.resid_dropout(self.c_proj(y))
        return y

Then in forward and backward propagation, attention is woven into loss function optimization

class Block(nn.Module):

    def __init__(self, config):
        super().__init__()
        self.ln_1 = LayerNorm(config.n_embd, bias=config.bias)
        self.attn = CausalSelfAttention(config)
        self.ln_2 = LayerNorm(config.n_embd, bias=config.bias)
        self.mlp = MLP(config)

    def forward(self, x):
        x = x + self.attn(self.ln_1(x))
        x = x + self.mlp(self.ln_2(x))
        return x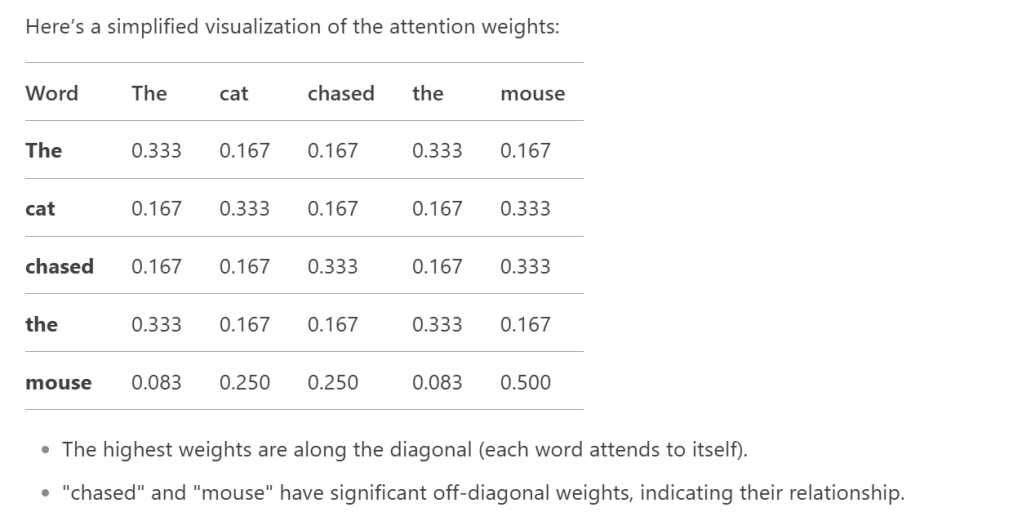

More directly interpretable from the output of the codes are

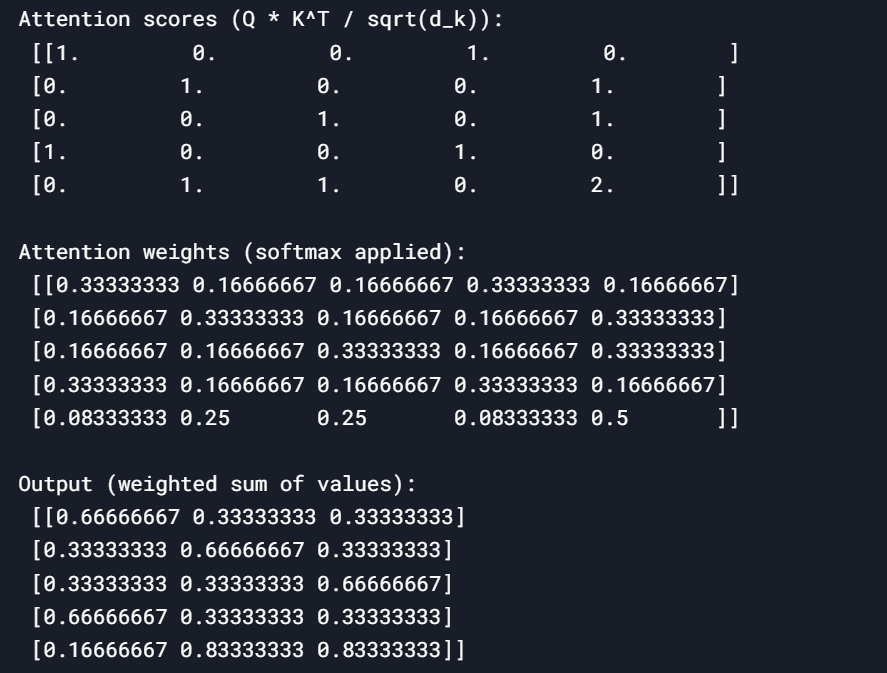
If we plot the visual of the vector position of the four words: the, cat, chase and mouse:

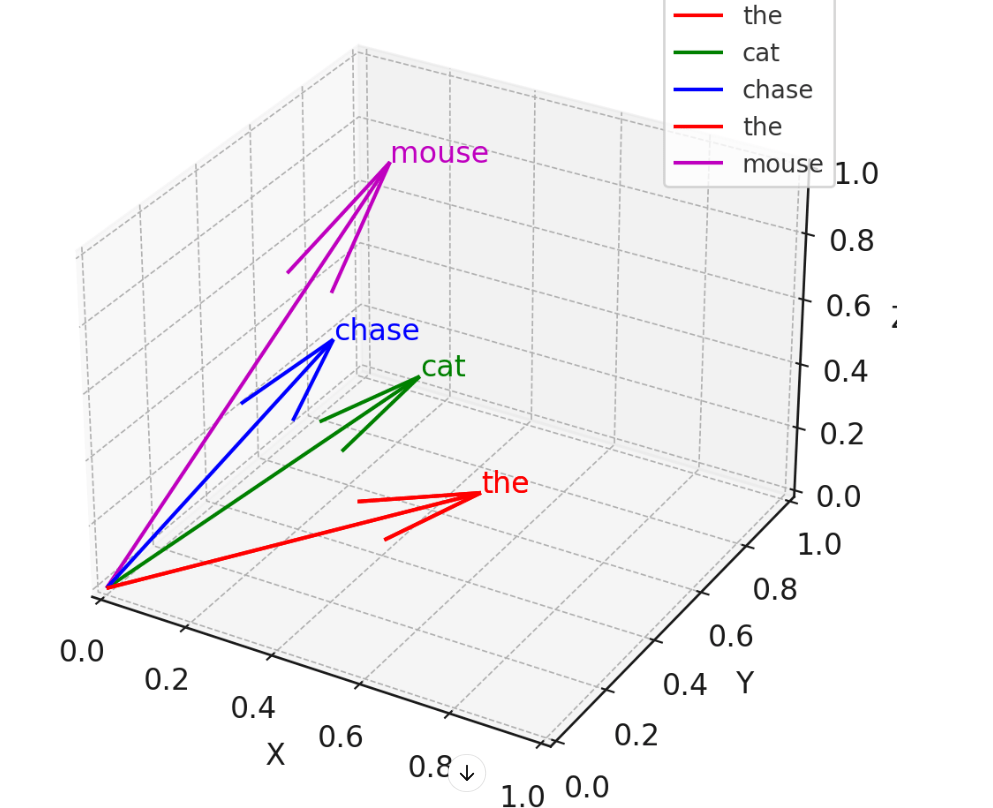
In the attention mechanism, the position of each word in the sequence is crucial because the order of words carries important information about the structure and meaning of the sentence. “The cat chased the mouse” is different from “The mouse chased the cat.” Without positional information, the model would treat both sentences identically, which is incorrect. However, in the basic implementation of attention (as shown in the previous code), the model does not explicitly account for word positions. To address this, positional encodings are added to the word embeddings to incorporate positional information.

There are two common approaches to positional encodings: Sinusoidal Positional Encodings (used in the original Transformer paper) and Learned Positional Encodings:These are learned embeddings for each position, similar to word embeddings.

The codes shall be revised to incorporate positioning information:

import numpy as np

# Step 1: Tokenize the input sentence
sentence = "The cat chased the mouse"
tokens = ["The", "cat", "chased", "the", "mouse"]

# Step 2: Define word embeddings (simplified for illustration)
embeddings = {
    "The": np.array([1, 0, 0]),
    "cat": np.array([0, 1, 0]),
    "chased": np.array([0, 0, 1]),
    "the": np.array([1, 0, 0]),
    "mouse": np.array([0, 1, 1])
}

# Convert tokens to embedding matrix X
X = np.array([embeddings[token] for token in tokens])
print("Embedding matrix X:\n", X)

# Step 3: Define sinusoidal positional encodings
def positional_encoding(max_seq_len, d_model):
    pos_enc = np.zeros((max_seq_len, d_model))
    for pos in range(max_seq_len):
        for i in range(0, d_model, 2):
            pos_enc[pos, i] = np.sin(pos / (10000 ** (i / d_model)))
            if i + 1 < d_model:
                pos_enc[pos, i + 1] = np.cos(pos / (10000 ** (i / d_model)))
    return pos_enc

# Add positional encodings to the embeddings
seq_len = X.shape[0]  # Sequence length
d_model = X.shape[1]  # Dimensionality of embeddings
pos_enc = positional_encoding(seq_len, d_model)
X_with_pos = X + pos_enc  # Add positional encodings to embeddings

print("\nPositional encodings:\n", pos_enc)
print("\nEmbedding matrix with positional encodings:\n", X_with_pos)

# Step 4: Define query, key, and value weight matrices (simplified)
W_Q = np.eye(3)  # Identity matrix for simplicity
W_K = np.eye(3)  # Identity matrix for simplicity
W_V = np.eye(3)  # Identity matrix for simplicity

# Step 5: Compute query, key, and value matrices
Q = X_with_pos @ W_Q  # Query matrix
K = X_with_pos @ W_K  # Key matrix
V = X_with_pos @ W_V  # Value matrix

print("\nQuery matrix Q:\n", Q)
print("\nKey matrix K:\n", K)
print("\nValue matrix V:\n", V)

# Step 6: Compute attention scores (Q * K^T / sqrt(d_k))
d_k = Q.shape[1]  # Dimensionality of key vectors
attention_scores = (Q @ K.T) / np.sqrt(d_k)
print("\nAttention scores (Q * K^T / sqrt(d_k)):\n", attention_scores)

# Step 7: Apply softmax to attention scores
def softmax(x):
    exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))  # Numerical stability
    return exp_x / np.sum(exp_x, axis=-1, keepdims=True)

attention_weights = softmax(attention_scores)
print("\nAttention weights (softmax applied):\n", attention_weights)

# Step 8: Compute weighted sum of values
output = attention_weights @ V
print("\nOutput (weighted sum of values):\n", output)

In Sum the extreme beauty is to use MATH to express and compute semantic/abstract information!