Math is a language and language can be simple and more sophisticated.

Based on Faraday’s discovery of electromagnetism, Maxwell came up with Maxwell equations, the vector calculus language to describe it, but when we elevate to 4D and leverage tensor and differential geometry to describe the same, we got more beautiful statement.

From Reumi’s world, I borrowed his derivation of how field tensor is to describe electromagnetism:

Further to deduce and it seems there are only two properties are required to describe it, which rank 2 tensor is ideal for:

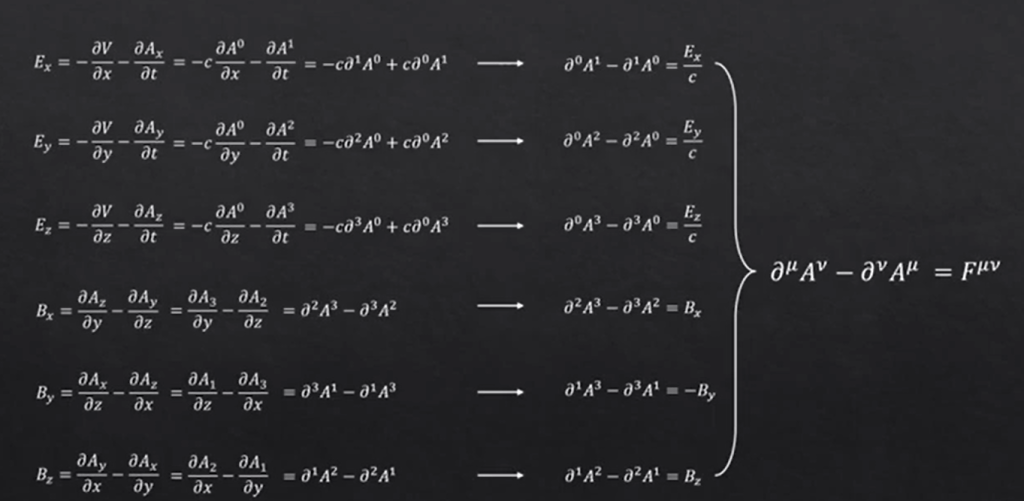
Next, we’d like to view electromagnetism in differential geometry:

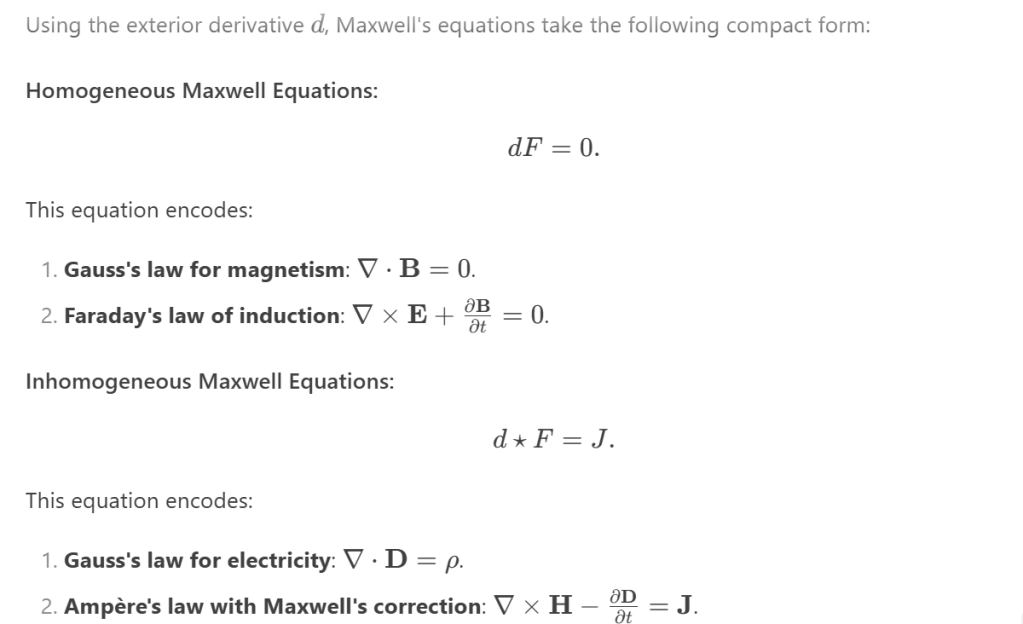
To deduce Maxwell’s equations in the language of differential forms using the exterior derivative, we start with the standard vector calculus form of Maxwell’s equations and systematically rewrite them in terms of differential forms. Here’s a step-by-step derivation:

First, Maxwell equation in vacuum with no sources are:

Then combines the electric field components (Ex,Ey,Ez) and the magnetic field components (Bx,By,Bz) into a single geometric object.

Then apply exterior derivate on this object F and expand it using product rule:

dF=d(Ex​dx∧dt)+d(Ey​dy∧dt)+d(Ez​dz∧dt)+d(Bx​dy∧dz)+d(By​dz∧dx)+d(Bz​dx∧dy).

dF=(∂y∂Ex​​dy+∂z∂Ex​​dz)∧dx∧dt+(∂x∂Ey​​dx+∂z∂Ey​​dz)∧dy∧dt+(∂x∂Ez​​dx+∂y∂Ez​​dy)∧dz∧dt+(∂t∂Bx​​dt+∂x∂Bx​​dx)∧dy∧dz+(∂t∂By​​dt+∂y∂By​​dy)∧dz∧dx+(∂t∂Bz​​dt+∂z∂Bz​​dz)∧dx∧dy.

…

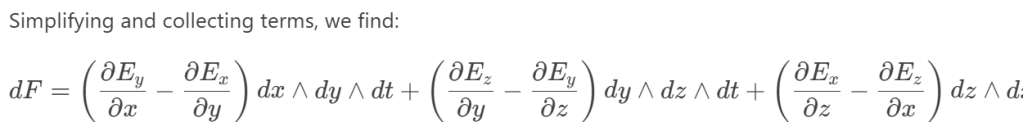
Note I omitted the intermediate deducing process (to be inserted later) and pasted here the hodge F’s corresponding matrix form:

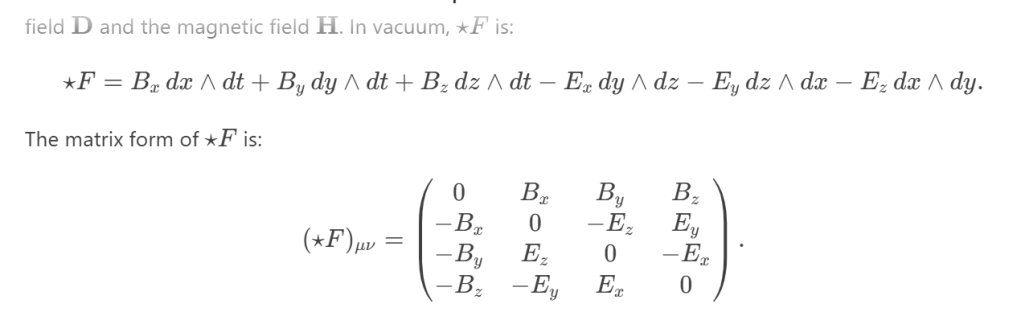
It makes Lorentz transformation easy and straightforward: