The key traits that an exceptional mathematician or physicist possesses include the ability to identify abstract similarities and commonalities between seemingly disparate objects. The concept of the “square root of geometry” in the context of describing spinors and supersymmetry serves as an exemplary illustration of this skill.

However these explanation from chatGPT is not intuitive. AI still can not replace the best brains of human beings.

Now there is a fun fact about algebras of the generators in Lie Group: commutator!

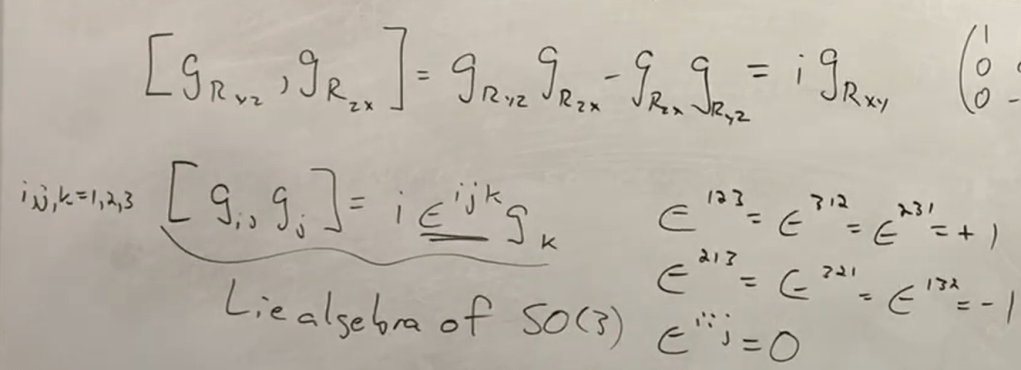
this will lead to the insightful spinor discovery and square root of geometry trait about spinor. By Alex Flournoy, we can start from the commutator characteristics and reason that a 2×2 matrix with imaginary number i in it can do the same and contains richer information and this matrix is square root of identity matrix:

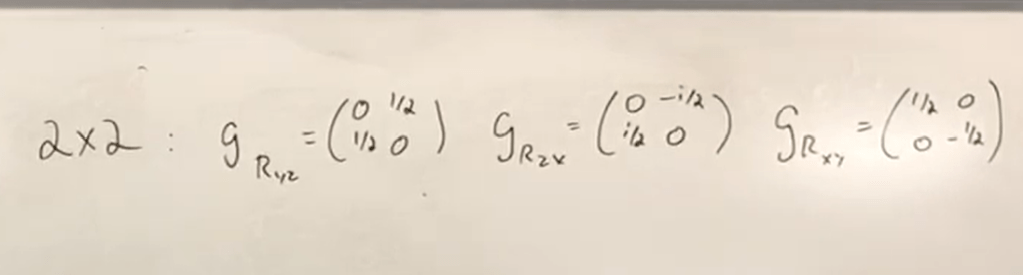
If we use this generator composed of angle theta, we don’t get exact same as 3×3 group SO(3), we need to double the angle to get to the origin. It’s not normal vector it’s a SPINOR in SU(2).