A comprehensive understanding of the ordinary derivative in flat space is well established; nevertheless, the requirement for the covariant derivative emerges from the characteristics of curved space. In our universe, specifically within the framework of space-time, spaces are intrinsically curved as opposed to flat. Accordingly, the derivative must incorporate the consideration that the basis vectors also change in order to accurately reflect this curvature.

For example, the constant component does not necessary mean the vector field is constant:

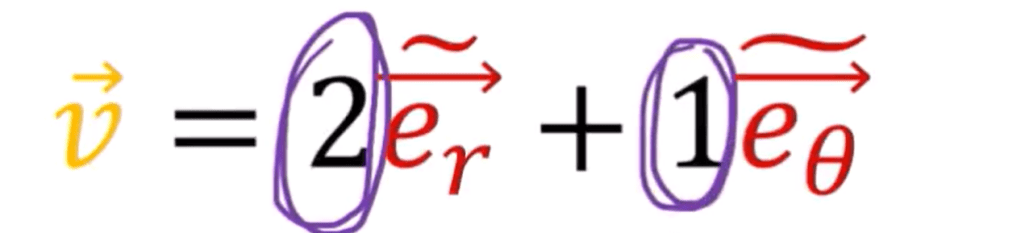
It is a very needed concept when we deal with curved space because it’s very hard to define a constant vector movement on a curved space, so we need to make it as much as possible – do parallel transport, where the vector rate of change(derivative) is always normal to the surface. hence covariant derivative is defined as below and if it’s zero then it’s doing parallel transport.

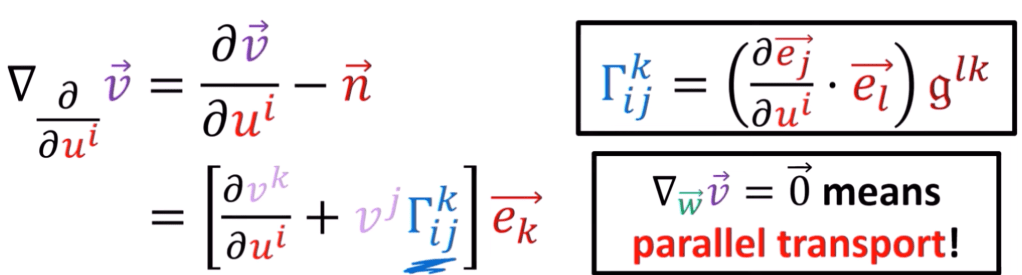
So these definition of covariant derivative leads to clear understanding of parallel transport and then geodesic, but how is it related to the gauge field in U(1) symmetry?

here is an abstract definition of covariant derivative

Because parallel transport provides a connection between between tangent spaces in a curved manifold, it’s actually covariant derivative should be called connection.

Note there are two important properties to utilize in computing torsion free and metric compatibility:

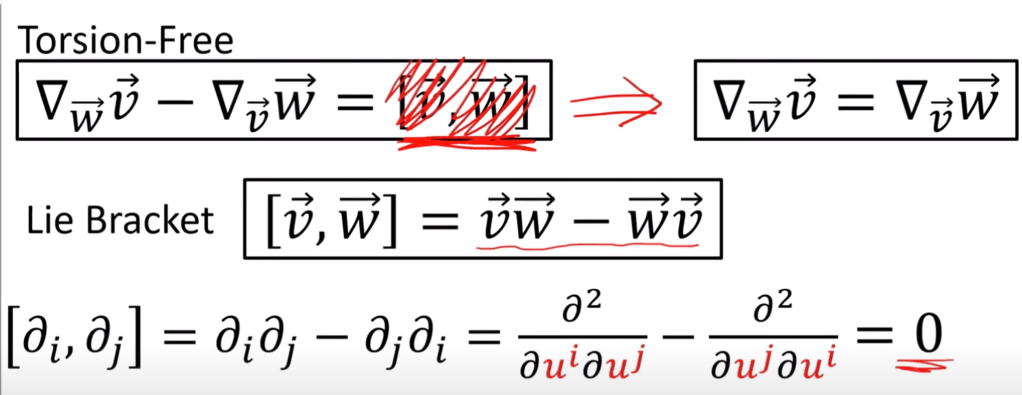
So we can say covariant derivative provides connection of tangent spaces, how is it also said connection of bundle fibers?