First of all, Geometry, bundles, differential manifolds, topological manifolds, topology, set theory and underneath the logic to build the mathematic edifice to understand truly law of nature: special relativity, classical physics, quantum physics, general relativity, chemistry and electromagnetism etc.

The paper’s content is as follows: the first filed theory on James Clerk Maxwell, Herman Weyl, Yang and Mills, the Gauge Theory, he emergence of a central mathematical construct
Abelian case on Magnetostatics, Adding Quantum Mechanics, Differential geometry for physicists and Back to EM
Non-Abelian case on differential geometry, general relativity and concluding remarks to a path to unification
Fiber bunder:
4.1 topological manifolds and bundles
4.2 principal and associated bundle
4.3 connections
4.4 parallel transport
4.5 curvature annd torsion on principal bundle
4.6 covariant derivatives

Great opening lines of this paper attracts my attention: “Since the early 20th century it has been understood that nature at the subatomic scale requires quantum mechanics, but the great breakthrough was the description of nature in terms of fields, led by Maxwell’s ingenuous achievements of unifying Electricity and Magnetism with light. Einstein followed, placing Space and Time at the same footing
relating them with matter through geometry. Herman Weyl tried to geometrize Maxwell’s theory in the same spirit of Einstein and opened the doors to gauge theories, which C. N. Yang and R. Mills used to generalized the concept to non-abelian gauge groups to account for the other two forces of nature, the Weak and the Strong. It was then shown that such gauge theories should be regarded as specific geometric constructs, namely fiber bundle manifolds.”

Faraday had his vague geometric conception of the “electro-tonic state” expressed in vol 3 p.443 he wrote: “. . . a state of tension or a state of vibration or perhaps some other state analogous to the electric current, to which the magnetic forces are so intimately related.” He believed that all metals take on the peculiar state of tension, appearing to be instantly assumed and he was perplexed by two facts: the magnet must be moved to produce induction and that induction often produce effects perpendicular to the cause. He was “feeling his way” in trying to understand electromagnetism, but today we have to “feel our way” in trying to understand his geometric intuition. Maxwell figured out in math, Maxwell carefully wrote: “. . . With respect to the history of the present theory, I may state that the recognition of certain mathematical functions as expressing the “electrotonic state” of Faraday, and the use of them in determining electrodynamic potentials and electromotive forces is, as far as I am aware, original; but the distinct conception of the possibility of the mathematical expression arose in my mind from the perusal of Prof. W. Thomson’s papers. . . ”

In 1861 and 1862, Maxwell wrote ““We can scarcely avoid inference that light consists in transverse undulation of the same medium which is the cause of electric and magnetic phenomena.” . In other words, light is equal to electromagnetic waves. This is a momentous discovery of great importance for humankind. Any person, religious or not, must stop and wonder, because one of the greatest secrete of nature was revealed. He wrote a very clear exposition of the basic philosophy of field theory: “In speaking of the Energy of the field, however, I wish to be understood literally. All energy is the same as mechanical energy, whether it exists in the form of motion or in that of elasticity, or in any other form. The energy in electromagnetic phenomena is mechanical energy. The only question is, where does it reside? On the old theories it resides in the electrified bodies, conducting circuits, and magnets, in the form of an unknown quality called potential energy, or the power of producing certain effects at a distance. . . on our theory it resides in the electromagnetic field, in the space surrounding the electrified and magnetic bodies, as well as in those bodies themselves, and is in two different forms, which may be described without hypothesis as magnetic polarization and electric polarization, or, according to a very probable hypothesis as the motion and the strain of one and the same medium.” Maxwell still believed there had to be an “aethereal medium” . Until Einstein’s 1905 special theory of relativity, according to which there is no “aethereal medium” , the electromagnetic field itself is the medium.

Maxwell’s equations have, beyond the Lorentz symmetry found by Einstein and Minkowski,
another symmetry, namely Gauge Symmetry, discovered mainly by H. Weyl in the years
1919-1929.

Every Lie group has some representation in different dimensions.
Weyl took this idea and published an important paper accepting that: Maxwell’s equations are invariant if one considers this combined gauge transformation. A precise definition in QM of gauge transformation both for EM field and for wave function of charged particles, a coupled transformation on one hand gives the EM transformation and on the other hand it changes the phase of charged particles in QM.

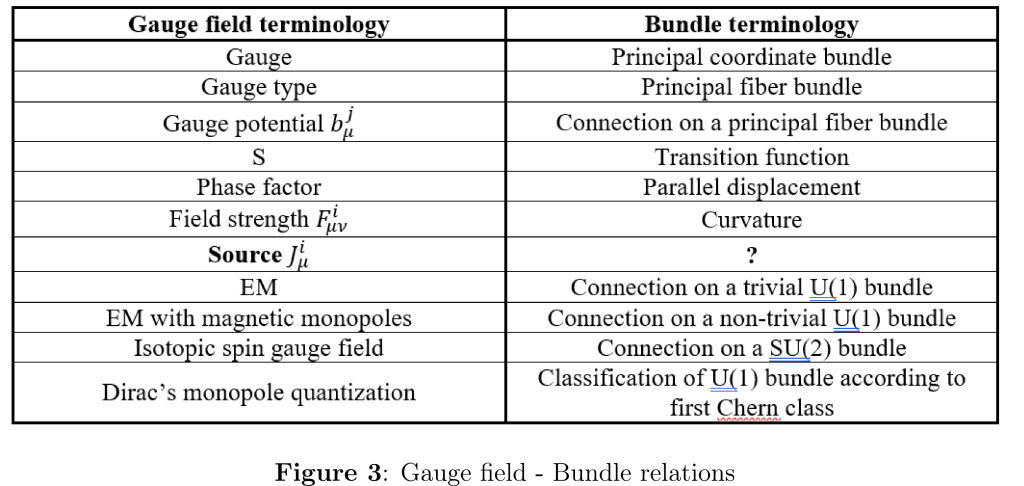
to be continued…