Homology provides a math way to define “holes” in a space. Hole is a loop that does not bound, i.e., the hole’s loop is not the boundary of anything else.

loop = collection of 1-cells with boundary zero. intuitively, we know that a hole is an unfilled region enclosed by a loop that cannot be contracted to a point within the space.

So we can extend the loop and hole concept to higher dimensional space,

The fundamental group of a space is a topological invariant that captures information about the space’s shape by describing its loops up to deformation.

however need to be group, so need to prove if it qualifies for group definition: identity, associative, inverse exists.

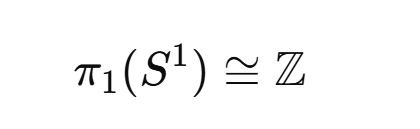
Examples

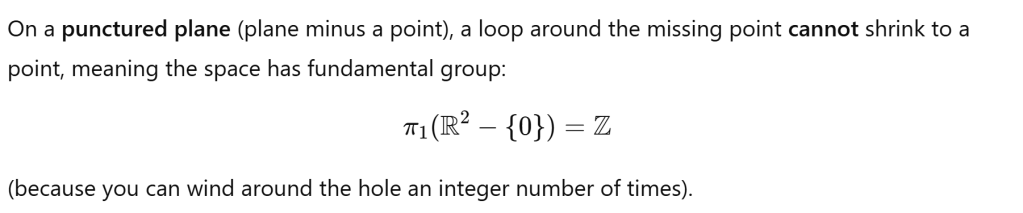
to be continued…

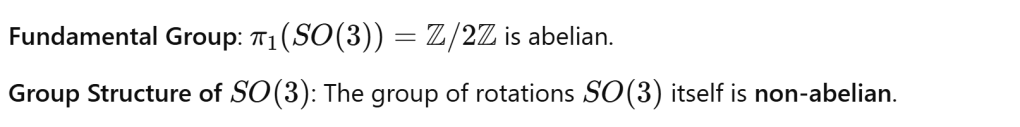
It’s quite hard to truly understand difference between a figure 8 and torus. one is non-abelian while the latter is abelian. The key is to think in torus, a smooth space, loop A and loop B can be deformed freely when you do AB or BA, it doesn’t matter!